W pierwszej części tego rozdziału opisałem fizyczne podstawy fiaska projektu KC PiS i pomocników, od dwóch lat próbujących wesprzeć błędnymi obliczeniami scenariusz wystrzelenia drzwi 2L tupolewa przez rzekomą eksplozję wewnątrz kadłuba samolotu i wbicia na 1 m pod ziemię. Swoimi wynikami udowodnili tylko to, że aby być inżynierem, trzeba znać fizykę.

Ściśle tajne
W jednej z samolotowych włóczęg z bratem nad bezdrożami i kolorowymi pustyniami Ameryki znanymi z westernów, lecieliśmy kilka lat temu nad kanionami (też tym wielkim kanionem Colorado), nad i pod formacjami skalnymi, jeziorami i tamami, po czym poprzez airspace class Bravo, nad hotelami-piramidami i kasynami Las Vegas, skierowaliśmy się na północny zachód. Okrążając The Box (zabronioną przestrzeń powietrzną 4808A wokół Area 51) musieliśmy ustalać gdzie usiąść, by nabrać paliwa po trwającym już wtedy ponad 3.5 godziny locie. Mogliśmy zejść z trasy w bok albo lecieć dalej "na styk" paliwa do Tonopah, którego wtedy nie znaliśmy. Było gorące popołudnie i trochę turbulencji w powietrzu. Nasze mierniki stanu paliwa nie dawały dokładnych wskazań. Inne urządzenie pomagało jednak potwierdzić ilość paliwa, mierząc tempo przepływu i sumując całkowite zużycie paliwa, ale żadne nie było precyzyjne. Pomyślałem, że można zyskać większą pewność o stanie paliwa. Trzeba zużyć wpierw praktycznie całą zawartość prawego baku... Udało się to trochę lepiej i szybciej niż myślałem. Silnik zgasł. Ożył po przełączeniu selektora paliwa na lewy bak. Od tej pory kurczowo trzymaliśmy się jedynej drogi przez pustynię w okolicy, prowadzącej do miasteczka, na wszelki wypadek ćwicząc w myślach lądowanie awaryjne.
Nie zapomnę miny operatora bazy obsługującego pompę paliwową, który aż gwizdnął na widok marnych kilku galonów benzyny lotniczej 100LL na danie lewego baku i sucho jak pieprz, zero, nada, w prawym. Zostało na 20 minut lotu - zamiast wymaganych 30 minut zapasu.

Wkrótce potem dowiedziałem się, że chwile niepewności co do pozostałego paliwa i mentalnej gotowości lądowania bez niego, nad tymi samymi pustyniami i pagórkami wokół Tonopah, dzieliłem z innymi pilotami, uczestniczącymi wcześniej w tajnym programie lotnictwa o kryptonimie Constant Peg (zob. wideo!) 4477 Szwadron Testów i Badań 'Red Eagles' prowadził coś w rodzaju programu szkolenia pilotów myśliwców TOP GUN z Miramar, ale w pustynnej okolicy, używając do tego autentycznych - kupionych, uprowadzonych, lub uszkodzonych i odrestaurowanych - radzieckich migów. Fascynującą historię programu relacjonuje książka Daviesa "Czerwone Orły. Tajne Amerykańskie Migi". Polecam! Zbieżność z naszym lotem polegała na tym, że niektóre migi (np. 23, 27) nie mają w ogóle mierników poziomu paliwa. Mają mniej pewny pomiar przepływu paliwa. Piloci Red Eagles nienawidzili tych samolotów, w odróżnieniu od Mig-21. Miały zmienną geometrię skrzydeł i były szybkie lecz mało zwrotne, zachowywały się niepokojąco w pewnych fazach lotu, przeciągnięcie w nich było tak brutalne, że konstruktorzy radzieccy zainstalowali na drążku sterowym klapkę. Jeśli kąt natarcia przekraczał 17 stopni, biła po kostkach, aż pilot odpuszczał nerwowo ciągnięty drążek. Za to można było w wolnej chwili słuchać rocka w radiu z Las Vegas. Oryginalne radia obejmowały cywilny zakres częstotliwości UHF w Ameryce. Odbyło się 15 tysięcy lotów, wyszkolono w walce z migami kilkuset pilotów. Aby trzymać wszystko w tajemnicy, piloci i mechanicy wychodzący do jedynej atrakcji w miasteczku (hotel z kasynem) nie mogli być w mundurach, ani wyglądać jak piloci. Rozkazano im zapuścić brody i wyglądać na robotników. Najciekawsze w ściśle tajnym programie Constant Peg było jednak to, że był przykrywką dla ukrytego pod nim jeszcze bardziej tajnego programu testowania w Tonopah i czasami w Area 51 "niewidzialnego" F-117 (latano nimi pod osłoną nocy; stąd i z niezwykłego kształtu latającego skrzydła wynikły moim zdaniem niektóre raporty o UFO). Na zakończenie dygresji zagadka: co to jest, niedaleko Tonopah? A teraz od migów powróćmy do tupolewa i danych przydatnych w testowaniu hipotezy wybuchowo-drzwiowej.
Poligon

Tonopah Test Range jako poligon do konstrukcji i badań polowych wszelkiego rodzaju bomb włącznie z termojądrowymi, założono w 1957 r. Zarządza nim rządowa agencja Sandia Ntnl Laboratories. Zrzucano je tam i testowano wszystko oprócz detonacji bomb jądrowych (co robiono na sąsiednich poligonach). Wbijano też w ziemię przeróżne rakiety i pociski artyleryjskie, testując ich zdolność przenikania gruntu, skał i umocnień. Raport Bernarda (1978), zalinkowany jak wiele innych źródeł w Bibliografii, zawiera używane zarówno metody modelowania ruchu wbijanych obiektów pod ziemią, jak i znaczą liczbę danych. Dokumenty pozwoliły mi skalibrować jeden ze współczynników metody opisanej w cz.1. Istnieje znaczna wiedza na temat zachowania gruntów przy prędkości zderzenia poniżej 100 m/s, i tą zajmiemy się dalej, w rozdz. 68.2 [służy m.in. do ustalenia σ(s)]. Jednak do wyznaczenia stałych dynamicznych przy v i v2 w formule na siłę oporu standardowa geotechnika ani inżynieria wbijania pali nie wystarczają; dlatego zaczęliśmy od poligonu TTR.
Armia USA zaprzecza fantazjom podkomisji
s(v) = 51.85 S N (M/A)0.7 ln (1 + v2/4647) dla v < 61 m/s, oraz (15a)
s(v) = 1.807e-5 S N (M/A)0.7 (v - 30.5) dla v > 61 m/s. (15b)
Czynnik N zależy od kształtu frontowej części pocisku; N = 0.56 w przypadku nieopływowego prostopadłościanu. Cała zależność głębokości penetracji od rodzaju penetrowanego materiału (np. rodzaju ziemi) jest linową zależnością daną wartością parametru S, daną odpowiednią tabelką w cytowanym raporcie. W przypadku gleby twardej, o dużej zawartości luźnego żwiru, ale nieskonsolidowanej, S = 4...6.Gleba piaszczysta ma S = 6...9. Typowa wierzchnia warstwa ziemi używana w robotach ziemnych ma S = 8...10, w zależności od ubicia. Gleba ilasta lub gliniasta, mało do średnio wilgotnej ma S = 5...10. Natomiast mokra gleba gliniasta, a także luźna warstwa wierzchnia (organiczna) ma S = 10...20. Najlepiej oddaje warunki w Smoleńsku wartość S ≈ 10..12.
Z równań (15) wynika, że kształt krzywej s(v) jest bardzo podobny do mojego modelu danego linią fioletową. Przy v > 100 m/s, moja zależność jest nieco nieliniowa a wzór Younga jest ściśle liniowy, ale ogólne dopasowanie do danych jest podobnej jakości. Przy masie drzwi 78 kg (rozsądnie proponowanej przez Olivaresa) i polu powierzchni bocznej wbijającej się w ziemię, 40 cm x 2 m = 0.4 m2, otrzymujemy przewidywaną przez formułę armii amerykańskiej głębokość penetracji drzwi 2L równą
s(140 m/s) = 1.807e-5 * (10...12) * 0.56 (78./0.4)0.7 * (140 - 30.5) = 0.44...0.53 m. (16)
Każda zmiana prędkości wbijania o 1 m/s powoduje zmianę drogi wbijania o 4.05 mm.
Należy zauważyć, że przy wbijaniu ukośnym, s oznacza drogę po skosie, zatem rzeczywista głębokość pod poziomem ziemi będzie mniejsza, gdy tor ruchu jest prostoliniowy i nieco odchylony od pionu. Jeśli jednak trajektoria pod ziemią nie jest prostą linią, a stopniowo zmniejsza nachylenie do horyzontu, co opisano w kilku raportach Sandia Labs, zaś początkowy kąt spadku ma tangens rzędu 70/140 (prawidłowa prędkość postępowa to ~70 m/s, założona pionowa ~140 m/s), to ostateczna głębokość H wbicia drzwi 2L staje się już mniejsza niż 89% wartości s, czyli mniej niż H = 39...48 cm pod powierzchnią ziemi.
To mniej niż pół metra, a więc nie spełnia to założeń błędnej hipotezy wybuchowej. Osiągnięcie wymaganego H ~ 1 m jest dużo trudniejsze. Do tego w Smoleńsku potrzeba wg wzoru Younga prędkości pionowej wbijania w ziemię drzwi 2L
v = 270 m/s = 972 km/godz. ==> H = 0.94...1.12 m (17)
Jest to nonsensowna propozycja wbijania drzwi prawie z prędkością dźwięku, wymagana przez ich zmyślony scenariusz, lecz nie uświadomiona przez podkomisję do spraw ponownej próby znalezienia zamachu. Dodatkowo, hipotezie wybuchowej zaprzecza to, że w rzeczywistości drzwi wciśnięte były pod ziemię bardziej pionowo. Zapewne dlatego podkomisja udaje, że prędkość postępowa wynosiła w momencie uderzenia w ziemię tylko 10 lub 20 m/s, mimo oczywistej sprzeczności z aerodynamiką.
Zobaczmy zaraz, że do podobnych, nawet jeszcze bardziej drastycznych konkluzji, prowadzą moje obliczenia.
68.2. PROBLEM DRZWI 2L
Dopasowanie parametrów teorii do danych z TTR
Poniższy rysunek pokazuje zbiór danych o głębokości (w metrach) zarycia pocisków o standardowych średnicach, w zależności od prędkości v (w m/s). Liną ciągłą pokazuję najlepsze dopasowanie rozwiązania równania (4) z cz.1 rozdziału, przy użyciu równań (5) i (6) wyprowadzonych w cz. 1.rozdziału, z następującymi parametrami: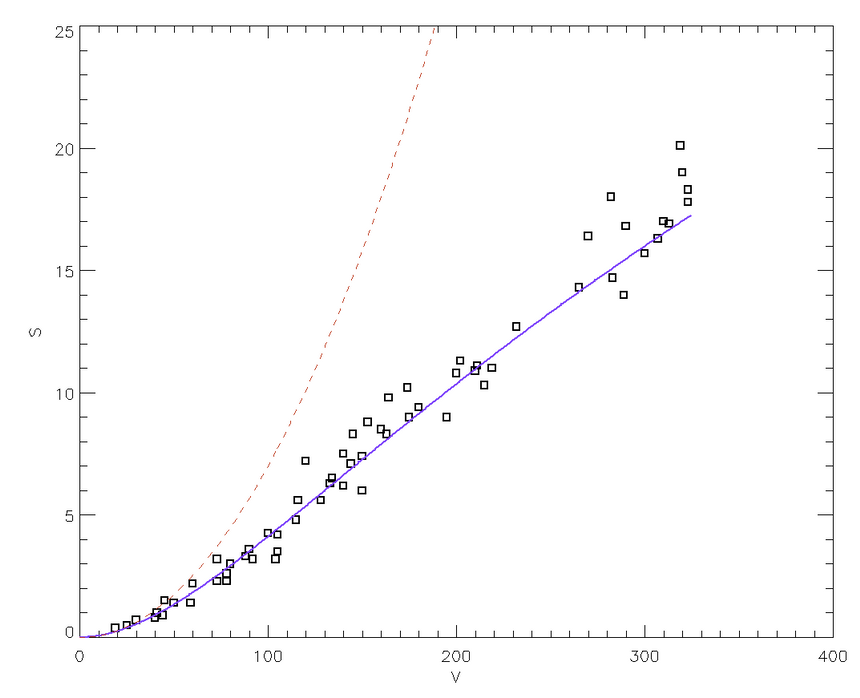
σ0 = 7.45 MPa h -> ∞ (tj. σ nie jest funkcją zagłębienia)
J = 0.0076 s/m Cd = 0.50 (ρ = 1600 kg/m3)
Oryginalne głębokości s(v) dotyczyły pocisków o nieco różnej masie i polu przekroju poprzecznego, dlatego zgodnie z oczekiwanym skalowaniem głębokości penetracji s wraz z M/A, zostały przeliczone do jednego standardowego kalibru i masy. Te wartości użyłem w procedurze dopasowania. Jak widać na pierwszym rysunku, wkład efektów zależnych od prędkości jest zawsze znaczący. Gdyby zaniedbać je, fioletowa krzywa stałaby się parabolą daną równaniem s(v) = (M/A) v2/2σ0 zaznaczoną przerywaną linią, i kompletnie nie zgadzałaby się z danymi eksperymentalnymi.
Balans trzech składowych naprężenia normalnego na powierzchni frontowej obiektu w moim modelu podaje następująca tabelka:
| Naprężenie: |
plastyczne |
~v (lepkość) |
~v2 (ef. inercyjny) |
w sumie |
| v = 50 m/s : |
σ0 = 7.5 MPa |
J σ0 v = 2.8 MPa |
Cd ρ v2/2 = 1 MPa |
11.3 MPa |
| v = 100 m/s : |
σ0 = 7.5 MPa |
J σ0 v = 5.6 MPa |
Cd ρ v2/2 = 4 MPa |
17.1 MPa |
| v = 140 m/s : |
σ0 = 7.5 MPa |
J σ0 v = 7.9 MPa |
Cd ρ v2/2 = 7.8 MPa |
23.2 MPa |
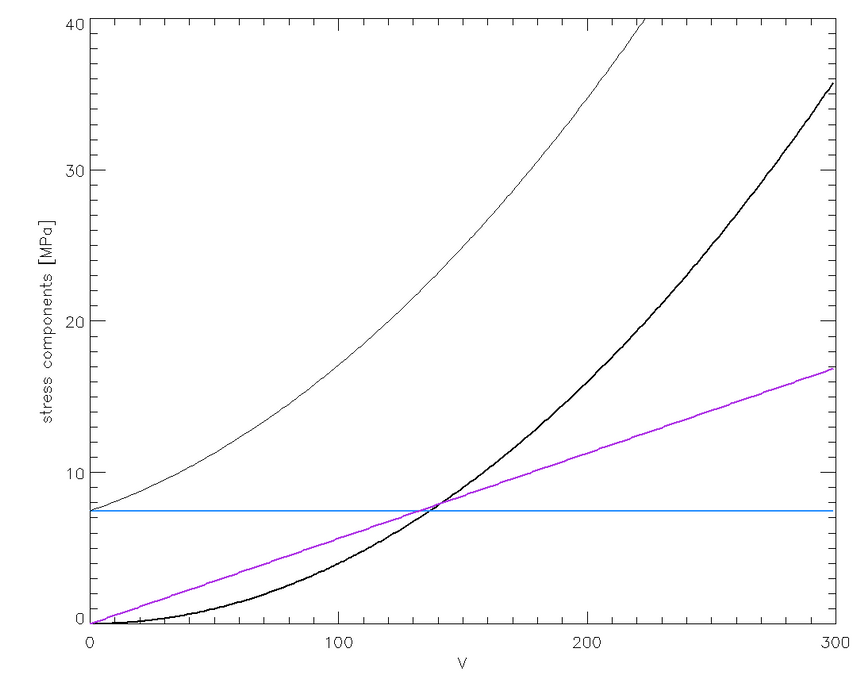
Ilustruje to dokładniej powyższy rysunek, pokazujący różnymi kolorami składowe ~v0, ~v1 i ~v2, oraz ich sumę (cienka czarna linia), dla różnych prędkości uderzenia.
Parametry gruntu
Możemy wykorzystać modele opisane w cz.1, sprawdzające się na poligonie TTR Sandia Labs, do rozsądzenia czy drzwi 2L mogły być wbite w ziemię na wrakowisku smoleńskim. Wartość wpółczynnika oporu czołowego (inercjalnego) równa 0.5 jest dość standardowa, można ją przyjąć bez obaw. Stałą Smitha J = 0.0076 s/m. Nie mamy pomiarów tego parametru w Smoleńsku, ale można go przyjąć także dla terenu smoleńskiego, gdyż pełen współczynnik pierwszej potęgi prędkości v we wzorze (6), będąc iloczynem σ0 i J, zależy od składu i wilgotności gleby poprzez σ0. To powinno wystarczyć do modelu hipotezy szybkiego wbijania drzwi w ziemię.
Wartość naprężenia σ0 tj. quasi-statycznego naprężenia plastycznego, zależy mocno od składu gleby i głębokości, która wynosi od 1 do 20 metrów pod ziemią w testach z Tonopah, a zaledwie 0-1 m w problemie smoleńskim. Dlatego ten parametr trzeba wziąć z innych badań, wilgotnej gleby, nie przypominającej pustyni. Parametr ten nie był w Smoleńsku badany i jest niepewny. Oczywiście obowiązek takich badań terenowych spada na proponujących możliwość wbicia drzwi na 1 m pod ziemię z prędkością 140 m/s.
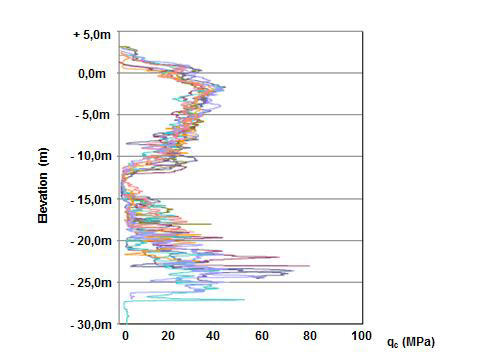
 Przyjrzyjmy się jakie wartości i ich rozrzut dostaje się typowo w metodzie CPT (Cone Penetration Test), stosowanej z powodzeniem od 40 lat. Głowica zanurzająca się w grunt jest wyposażona w sensory naprężeń: zarówno czołowego, jak i ścinania na powierzchniach bocznych obiektu. Na tej podstawie CPT identyfikować może rodzaje gruntu w warstwach zalegających do głębokości 20, nawet 30 i więcej metrów. Ziemia jest taka różnorodna, że zobaczyć możemy w literaturze bardzo różne wyniki pomiarów σ0 w warstwie przypowierzchniowej, od < 1 MPa, aż do 10 MPa i więcej. Oto przykłady indywidualnych pomiarów, jak i kompilacje wielu testów CPT.
Przyjrzyjmy się jakie wartości i ich rozrzut dostaje się typowo w metodzie CPT (Cone Penetration Test), stosowanej z powodzeniem od 40 lat. Głowica zanurzająca się w grunt jest wyposażona w sensory naprężeń: zarówno czołowego, jak i ścinania na powierzchniach bocznych obiektu. Na tej podstawie CPT identyfikować może rodzaje gruntu w warstwach zalegających do głębokości 20, nawet 30 i więcej metrów. Ziemia jest taka różnorodna, że zobaczyć możemy w literaturze bardzo różne wyniki pomiarów σ0 w warstwie przypowierzchniowej, od < 1 MPa, aż do 10 MPa i więcej. Oto przykłady indywidualnych pomiarów, jak i kompilacje wielu testów CPT.
Zacznijmy od typowych, czasami mocno piaszczystych gruntów przypowierzchniowych. Nasze σ0 oznaczane bywa σT, qt, lub podobnie. Jednostką jest MPa.
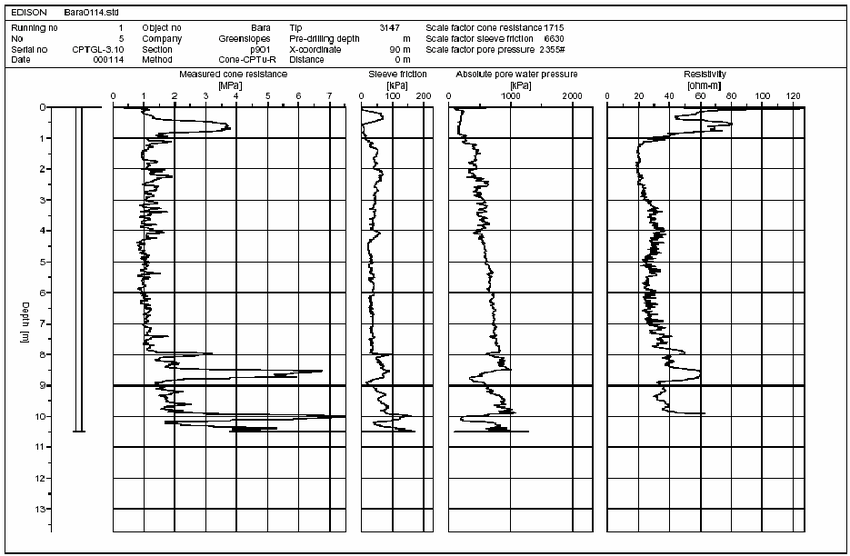
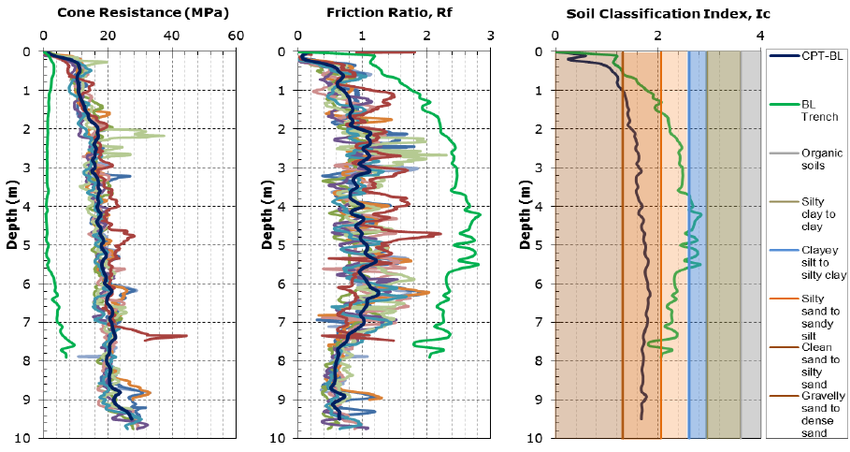
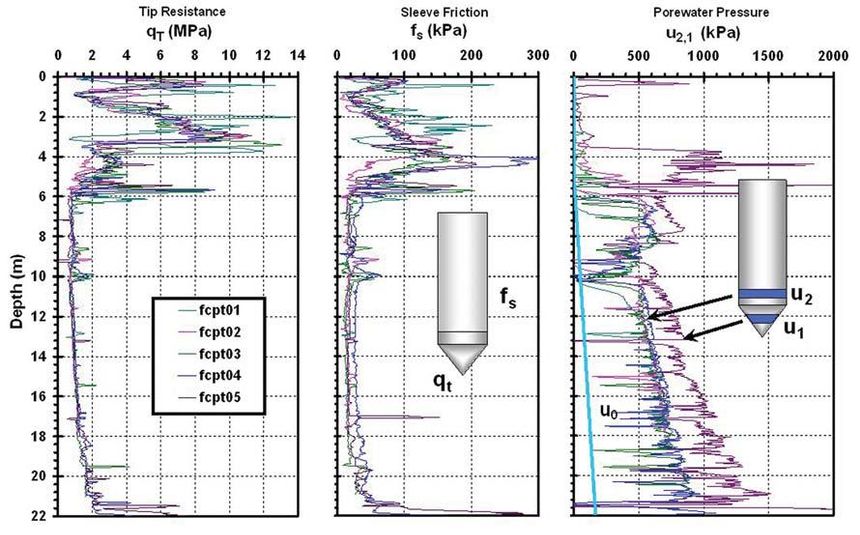
Bardziej zbliżone do właściwości smoleńskiej gleby są te pomiary warstw z zawartością drobnego piasku i iłu, gliniaste i uwodnione:
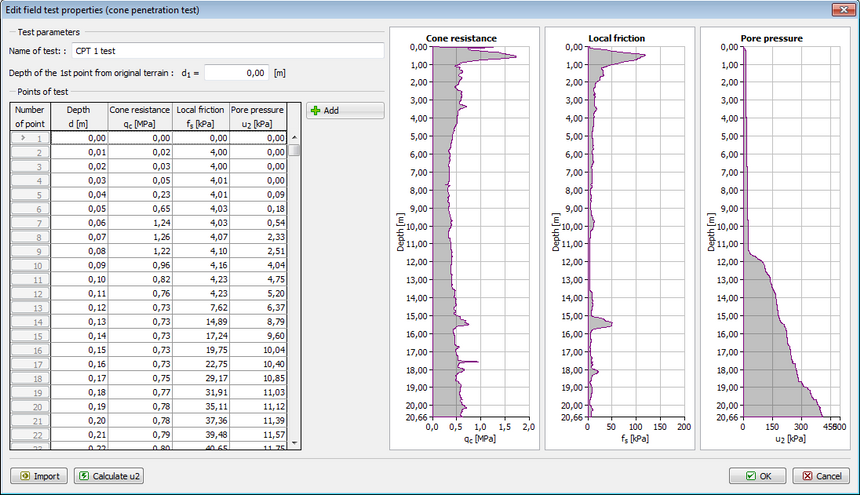
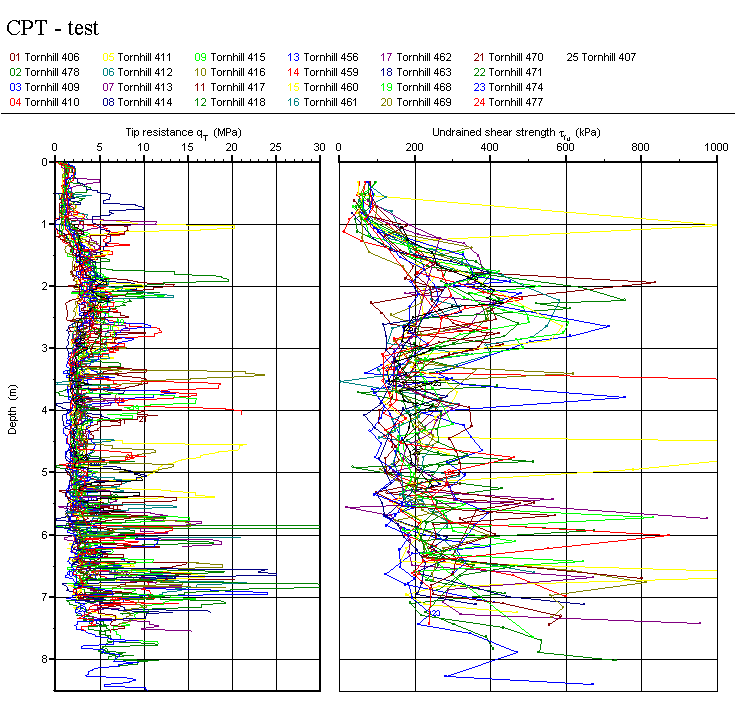
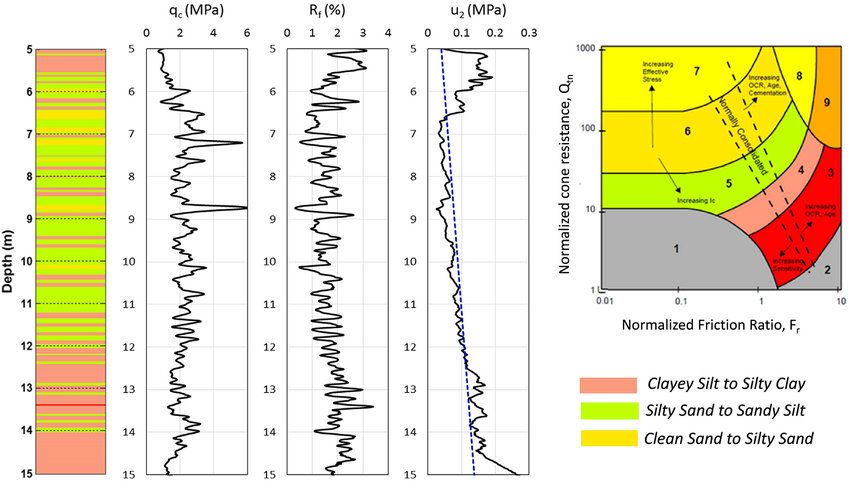
Tutaj np. poniżej 4 m pod powierzchnią zalega w miejscowości Amherst stosunkowo plastyczna glina (σ ~ 0.5 MPa).
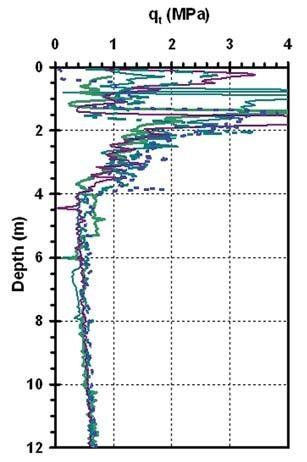
Na podstawie przeglądu literatury wezmę następujący zakres prawdopodobnych smoleńskich wartości σ0 w warstwie do 1 m głębokości, gęstości gruntu, oraz typowego h (różnicę głębokości na jakiej σ rośnie o σ0):
σ0 = 0.75....1.5 MPa, ρ = 1700 kg/m3, h = 3 m (18)
Przyjęta wartość h zmienia wyniki tylko umiarkowanie, gdyż oznacza, że gradient naprężeń nie jest stromy. Dlatego nie rozważam zakresu tego parametru, tylko rozsądną wartość. Gęstość wilgotnego gruntu jest oszacowana na podstawie literatury i jest niepewna < 10%.
Wyniki modelu
Podobnie jak w poprzednim podrozdziale, przyjmę pole powierzchni drzwi 2L A=0.4 m2, oraz masę M = 78 kg. To i znajomość czterech parametrów gruntowych: σ0, J, Cd, oraz h, wystarcza do wyznaczenia s(v) z teorii przedstawionej w cz. 1 rozdziału (równania 5-8a).
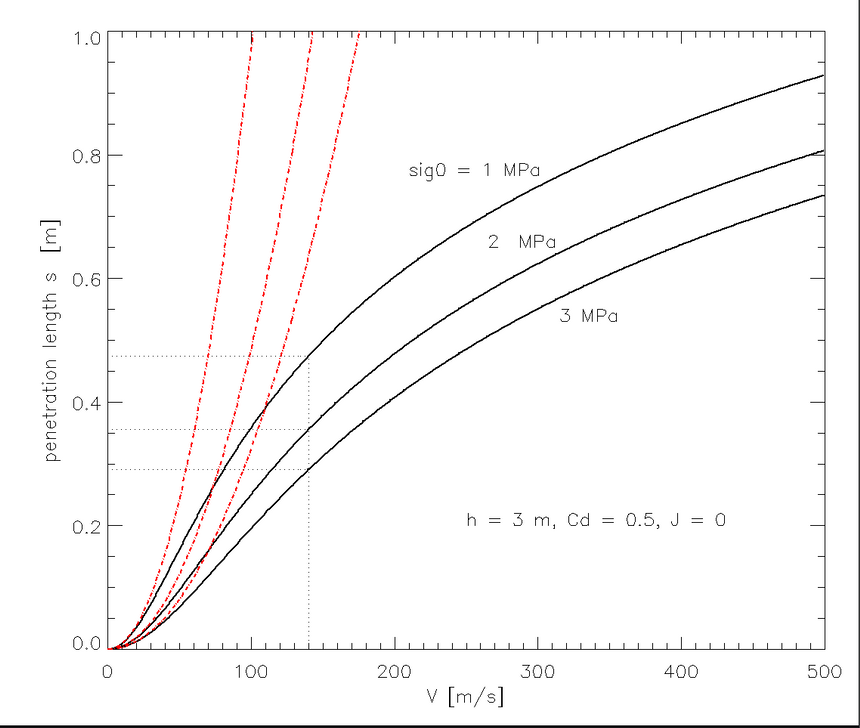
Gdybyśmy popełnili błąd, uznając opór ośrodka za niezależny od prędkości, proponowana w hipotezie wybuchowej prędkość zderzenia 140 m/s zapewniłaby drogę hamowania s=1 m przy naprężeniu statycznym σ0 = 2 MPa. Wystarczy jednak uzupełnić opór o konieczny fizycznie efekt inercjalny, a dla zakresu σ0 = 1..3 MPa otrzymamy drogę hamowania od 0.30 do 0.48 m, podobną do wyznaczonej z metody Younga.
A teraz uwzględnimy wszystkie trzy składowe oporu. Wyniki wykreślone są poniżej kolorem czarnym i pokazują s(v). Na czerwono zaznaczona jest na osi prędkość dźwięku Vs. Otrzymaliśmy drogę hamowania s(140 m/s) = 0.35...0.45 m. To wynik zgodny z obliczonym wg metody US Army.
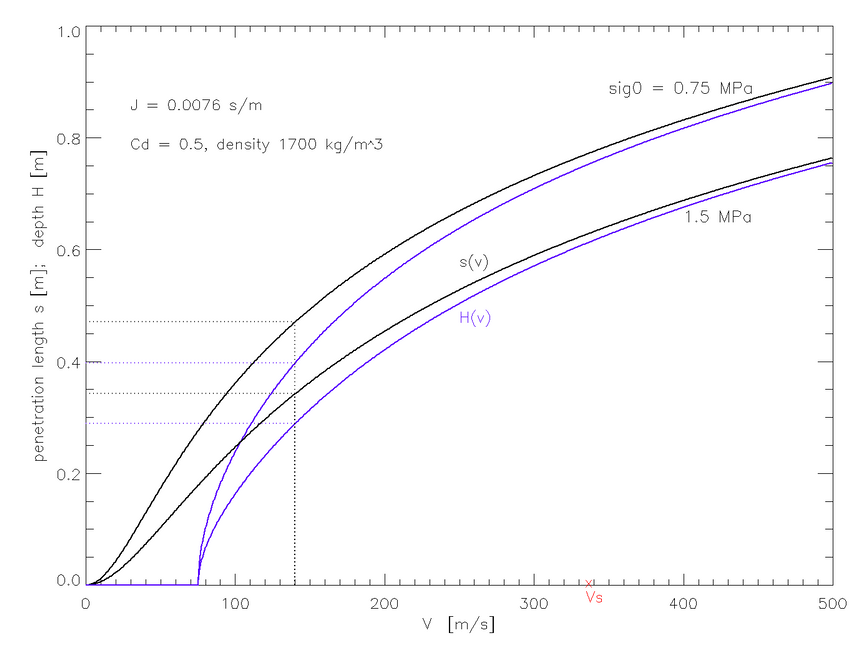
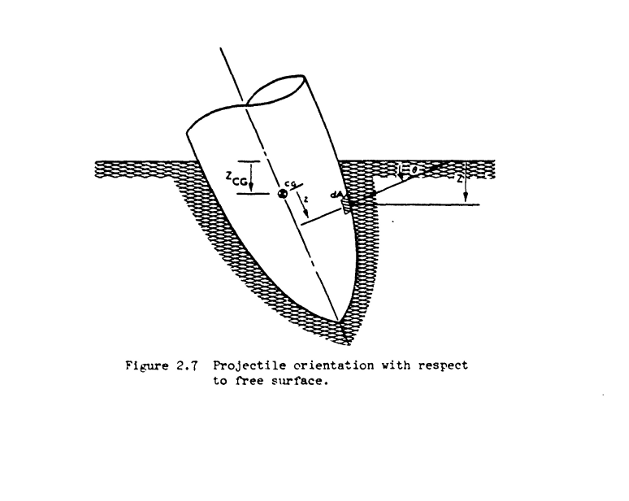
Weźmy pod uwagę geometrię zderzenia. Jeśli w momencie wybuchu samolot porusza się z prędkością poziomą
u = 75 m/s, (19)
a drzwi uderzają z prędkością v, to trajektoria hamowania pod ziemią nachylona jest do pionu pod kątem, którego sinus równy jest u/v (aby otrzymać prędkość zderzenia z animacji podkomisji v = 140 m/s, trzeba rozważać prędkość pionową wystrzelenia drzwi ku ziemi (v2 - u2)1/2 = 118 m/s). Trajektoria odchylona jest o arcsin(75/140) = 32 stopnie od pionu. Zatem aby otrzymać głębokość H utknięcia framugi bocznej drzwi pod ziemią, trzeba wartości s(v) jeszcze pomnożyć przez czynnik cos(32 st.) = 0.84 w proponowanym scenariuszu v. Ogólniej
H(v) = (1 - u2/v2)1/2 s(v). (20)
Rzeczywista głębokość H pod ziemią może być jeszcze nieco mniejsza, jeśli trajektoria wygina się w kierunku powierzchni ziemi (Bernard & Creighton 1979), nie jest jednak jasne czy to zaszłoby w przypadku drzwi 2L.
Dyskusja wyników
Fioletowe krzywe pokazują maksymalną głębokość H(v) do której mogły dotrzeć drzwi 2L, przy uwzględnieniu oporu dynamicznego gleby smoleńskiej. Zaczynają się od v=u=75 m/s, bo wolniej niż samolot drzwi nie mogły lecieć (zaniedbuję opór powietrza, gdyż jedyna szansa znalezienia drzwi w osi wrakowiska istnieje wtedy, kiedy wybuch zachodzi na bardzo małej wysokości, dosłownie kilku m). Gdy v~u, to spadek jest bardzo płaski, czyli H prawie zerowe. Zatem krzywe H(v) leżą poniżej czarnych krzywych, gdyż trajektoria drzwi nie była pionowa. W warunkach scenariusza wybuchowego maksymalne zagłębienie pod powierzchnię ziemi to H = 0.30 do 0.48 metra. A to, podobnie jak empiryczne wyniki armii amerykańskiej (dające rezultat 0.39 do 0.48 m) obala hipotezę wybuchowego wbicia drzwi 2L w ziemię. Aby w hipotetyczny sposób drzwi zagłębiły się bokiem na 1 m pod ziemię, potrzebna byłaby sporo ponaddźwiękowa prędkość wyrzucenia przez wybuch. W rzeczywistości, jak pisałem w cz.1, zarówno tak wielka prędkość, jak i proponowana v = 140 m/s, są nonsensowne, albowiem pęd przekazany przez falę uderzeniową eksplozji dużej bomby termobarycznej drzwiom nie powoduje wyrzucenia z prędkością większą niż 10 m/s, i to też przy specjalnych, wątpliwych założeniach. Po realnym wybuchu, drzwi wbijałyby się płasko z prędkością v ~ u ~ 70 m/s, i w najlepszym razie zostawiły bruzdę o głębokości H < 5 cm w ziemi.
Przypomnę też w końcu to, o czym mówiłem kilka lat temu na obradach komisji sejmowej: jeśli w tupolewie nastąpiłby wybuch zdolny "wystrzelić" drzwi 2L, to cały szereg innych części tupolewa także byłoby "wstrzelonych" w ziemię lub "wystrzelonych" na duże odległości. W szczególności, prawe drzwi poleciałyby bardzo daleko poza ograniczone do normalnych w katastrofach lotniczych rozmiarów pole rozpadu PLF 101. Prawe okna też wyleciałyby z framug z hukiem i szukalibyśmy ich gdzieś daleko. Wszystkie bez wyjątku dowody rzeczowe przeczą przewidywaniom hipotezy wybuchowej. Odpowiednie obliczenia pozostawiam zainteresowanym (zrobił je p. M. Jaworski, ale można spróbować osobiście. Trzeba naturalnie uwzględnić właściwie siły aerodynamiczne).
68.3. PODSUMOWANIE ROZDZIAŁU
- Przedstawiłem w tym rozdziale analityczną teorię wbijania przedmiotów w gęsty ośrodek typu ziemi, która może być też stosowana do innych celów niż weryfikacja hipotez smoleńskich. Oparta jest na bogatej literaturze dot. tego typu teorii tworzonych w przeszłości, jednak na ogół pomijających niektóre szczegóły fizyki hamowania w ośrodkach ciągłych lub granularnych. Na przykład, inżynieria konstrukcji palowych dobrze daje sobie radę wyliczając opór jako statyczny plus dynamiczny, wprost proporcjonalny do prędkości razy stała Smitha "J", zaś wojskowa balistyka końcowa dawała sobie od dawna nieźle radę zaniedbując ten człon równań i tylko biorąc pod uwagę opór inercjalny ~v2 (Poncelet 1839). Moje obliczenia zawierają oba człony oporu dynamicznego, a także stały opór quasi-statyczny (przegląd zagadnień szybkiego wbijania w ziemię zawiera książka Iskandera i in. (2015).
- Wyniki, które otrzymałem zgodne są z danymi z poligonu doświadczalnego w Tonopah, NV, tak samo dobrze jak empiryczne dopasowanie uzyskane w latach 70-tych przez wojsko amerykańskie (Young 1997). Formuła Younga przewiduje wbicie drzwi 2L w proponowanych warunkach na 39 do 48 cm pod ziemię.
- Stosując parametr Smitha oraz współczynnik oporu czołowego Cd (mnożący v2), uzyskane z dopasowania do danych amerykańskich, zaś osobno σ(s), quasi-statyczny opór gruntu o właściwościach zbliżonych do tego, co wiemy o rejonie katastrofy komunikacyjnej w Smoleńsku, uzyskałem wykresy pokazujące końcowe zagłębienie drzwi 2L w scenariuszu, gdzie wybuch w kadłubie wbija je pod ziemię. Zarówno wzory Younga, jak i moje wyniki pokazują, że drzwi w proponowanej hipotezie wybuchowej nie mogą zagłębić się więcej niż pół metra pod ziemię (dokładniej 30 do 48 cm). Zagłębienie na metr pod ziemię nastąpiłoby nie przy proponowanej prędkości początkowej v=140 m/s, a przy prędkości dźwięku lub ponaddźwiękowej. (To też jest wykluczone, bo drzwi byłyby wtedy znacznie bardziej zgniecione).
- Istnieje cały długi szereg dowodów wymienionych w tym rozdziale na to, że ani wystrzelenie drzwi z tupolewa rządowego, ani ich wbicie zgodnie ze scenariuszem sugerowanym przez tzw. podkomisję smoleńską nie było fizycznie możliwe. Nie dziwi to, gdyż ta jaczejka ma na swym koncie już cały szereg innych nonsensownych hipotez. Jest to bardzo słabe ramię pseudonaukowe jednej z partii politycznych. Wiceprezes kieruje oszustwami oraz zatrudnia za publiczne pieniądze niefachowych kontrahentów na zasadach sprzecznych z badaniami naukowymi, nie ujawniając marnotrawionego budżetu (wbrew orzeczeniu sądu).
(c) P. Artymowicz, 10 września 2020 r.
68.4. BIBLIOGRAFIA
R. Bernard, "Depth and motion prediction for earth penetrators", Technical Report S-78-4, Office of Engineers, U.S. Army (1978), (link)
S. Davies, "Red Eagles. America's Secret Migs", Osprey Publ. (2008) (link w tekście rozdz.)
M. Iskander, S. Bless, M. Omidvar, "Rapid penetration into granula media: Visualizing the fundamental physics of rapid earth penetration", Elsevier (2015)
L. Johnson, "Tonopah Test Range. Outpost of Sandia National Laboratories", DOE Oak Ridge (1996) (link)
C. Young, "Penetration Equations", CONTRACTOR REPORT SAND97-2426, Sandia Labs, (1997) (link)
R. Bernard, D. Creighton, "Projectile penetration in soil and rock: analysis for non-normal impact", Sandia Labs (1979), (link)
M. Forrestal, V. Luk, "Penetration into soil targets", Int. J. Impact Engn 9 Vol 12, No, 3. pp 427-444, (1992)
J. Poncelet, "Introduction Ii la Mecanique Industrielle",. Meline, Cans et compagnie, Brussels, (1839)















Komentarze
Pokaż komentarze (37)