Mathematica w działaniu

Taki Euler czy Jacobi mieli o wiele bardziej rozwinięte mózgi niż ja. Co ja rachuję programem, oni rachowali w pamięci. Ja w pamięci nic wyrachować nie potrafię. Nawet z programem nie zawsze mi idzie. Język C mi jakoś nie pasuje. Fortran dobrze rachuje na liczbach, ale rysować nim to udręka. W dodatku symbolicznie coś wyrachować to niemożliwe. Najbardziej pasuje mi program Mathematica Wolframa. Więc co można to liczę i symuluję przy użyciu tego właśnie programu. Oczywiście prawie wszystko co da się zrobić Mathematiką, da się też w miarę zgrabnie zrobić przy pomocy programów Maple czy Matlab. Ostatnio skoncentrowałem się jednak na tym jednym: Mathematica. No i dziś rachuję i pokazuję rozwiązania równań Eulera i fikołki gajki Dżanibekowa.

Rozwiązania równań Eulera dyskutowaliśmy w poprzednich dwóch notkach. Przyjrzyjmy się tym rozwiązaniom bliżej. Oto animacja, a pod nią mój kod dla programu Mathematica tę animację robiący i zapisujący na dysk.

 

Wybrałem momenty bezwładności I1=1, I2=2, I3=3 – do modelowania fikającej gajki w sam raz. Widzimy, że parametr d dający stosunek podwojonej energii kinetycznej do kwadratu krętu jest tu 0.35. Kwadrat krętu przyjmuję równy 1. d musi się zawierać pomiędzy 1/I3=0.333.. oraz 1/I1=1. 0.35 jest zatem blisko dolnej dolnej granicy. Przy danym kręcie niewiele możemy jeszcze dalej odjąć nieco energii kinetycznej – „kółko” można zmniejszyć do punktu, gdy już nie ma żadnej precesji a jest tylko wirowanie wokół osi z największym momentem bezwładności.

Zasadnicza część programu, symulująca ruch, kończy się na formule na m3. Potem jest formuła na wyliczenie okresu - oznaczyłem go jako tf. Dalej maluję przecięcie sfery jednostkowej z elipsoidą stałej energii (cp – plot konturowy), parametryzuję ruch wyliczając położenia co 1/10 okresu, no i zapisuję jako animowany gif.

Ten sam kod, tylko z d=0.95 daje precesję względem pierwszej osi:

Gdy d, co to u nas musi się zawierać pomiędzy 0.333... a 1.0, gdy więc jego wartość zaczyna się zbliżać do 1/I2=0.5, wtedy zaczyna się fikanie. W którym momencie kończy się precesja a zaczyna fikanie? Nie potrafię tego zdefiniować. Przejście wydaje się być płynnym. Oczywiście fajnie by było zobaczyć na animacjach co się dzieje? Nic trudnego. Ten sam kod, tylko wartość d zmienić na początku! Oto d=0.4999

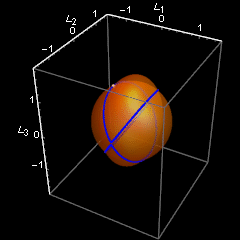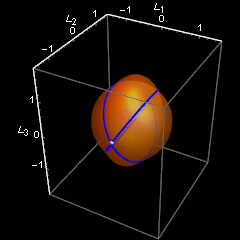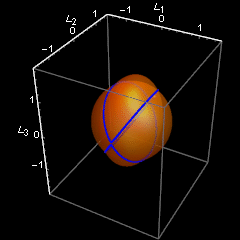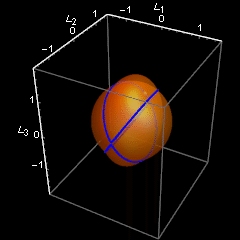
Czym bardziej zbliżamy się do d=0.5, tym dłużej trwa przebywanie w pobliżu końców drugiej osi, i tym krócej trwa fikołek - przejście na drugi koniec. Dla d dokładnie równego 0.5 jest tylko jeden fikołek, z jedengo końca na drugi. Jednak by ten przypadek objąć, trzeba napisac osobny kod, bowiem mój kod napisałem jedynie dla ruchów okresowych, gdy tf jest skończone.