Rozważał sobie Felix Klein (to nikt inny, to właśnie on, w dzieciństwie, był na portrecie z poprzedniej notki) równanie w trzech zmiennych zespolonych x,y,z. A równanie było czwartego stopnia i w dodatku całkiem symetryczne:
x3y+y3z+z3x = 0.
Trzy zmienne, czwarty stopień, razem siedem, nieprawdaż? I faktycznie, wyszło siedem, wyszło 168 = 23x 3 x 7 i wyszły inne cudeńka. Podsumowująca praca Felixa Kleina, w tłumaczeniu na język angielski, znajduje się w tomie „The Eightfold Way”, MSRI Publications, Volume 35, 1998.
MSRI to Mathematical Sciences Research Institutew Berkeley, California, tam też znajduje się rzeźba pokazana w mojej poprzedniej nocie. Rzeźbę wykonał artysta Helaman Ferguson, a pracę sponsorował koncern Mitsubishi Electric. Przeszukując obrazki w Google z hasłem „Klein'sQuartic„ można znaleźć wiele pięknych obrazków. Postanowiłem zatem i ja swój własny, może nie aż tak piękny, wyprodukować. Instrukcje znalazłem w pracy „The Riemann Surface of Klein with 168 Automorphisms”, autorami są H.E. Rauch i J. Lewittes, a praca sponsorowana była przez Air Force Office of Scientific Research, Office of Aerospace Research, United States Air Force. Ciekawe, czemu lotnictwo interesuje się takimi dziwnymi rzeczami, nieprawdaż? Czemu uważa je za godne swoich pieniędzy? No, ale to temat nie na teraz. Fragment z instrukcjami znajduje się poniżej. Przytaczam:
The Riemann Surface of Klein with 168 Automorphisms
HARRY E. RAUCH1 AND J. LEWITTES
1. Introduction
In the following we consider Klein's compact Riemann surface of genus three admitting a simple group of kl2168 automorphisms (conformal self-homeomorphisms) and adduce certain of its properties which to our knowledge and, indeed, surprise do not seem to be in the literature.
...
From the time of Hurwitz's fundamental researches (see [6]), on Riemann surfaces with nontrivial automorphisms Klein's surface has served as the most pregnant illustration of the phenomenon; thus, for example, it was until recently the only known surface for which Hurwitz's bound of
1Research partially sponsored by the Air Force Office of Scientific Research, Office of Aerospace Research, United States Air Force, under AFOSR Grant No. AF-69-1641.
297
….We call attention to an incorrect answer to (iii) by Hurwitz ([7], p. 159, criticized in [1]) and an abortive attempt on (i), (ii), and (iii) by Poincare in [16], p. 130, all noticed after the completion of our work.2
2. Klein's surface
Klein originally obtained his surface S in the form of the upper half-plane identified under the principal congruence subgroup of level seven, Gamma(7), of the modular group Gamma. In this form it is necessary to compactify the fundamental domain at its cusps. Klein's group then appears as Gamma/Gamma(7), which is simple and of order 168.
We need, however, another representation given by Klein, one which we recognize today as the unit circle uniformization of S. In the unit circle draw the vertical diameter L1and another diameter L3 making an angle of Pi/7 with L1 and going down to the right. In the lower semicircle draw the arc L2of the circle which is orthogonal to the unit circle and to L1and which meets L3at the angle Pi/3. Let t be the non-Euclidean triangle enclosed by L1,L2,L3 and let RuR2iR3be the non-Euclidean reflections in L1,L2,L3respectively. R1,R2,R3 generate a non-Euclidean crystallographic group, which we denote by (2, 3, 7)', with t as a fundamental domain. The images of t under (2, 3, 7)' are a set of non-Euclidean triangles each of which is congruent or symmetric to t according as the group element which maps t on it has an even or odd number of letters as a word in R1R2iR3. These triangles form a non-Euclidean plastering or tesselation of the interior of the unit circle. The union of t and its image under R2is a fundamental domain (with suitable conventions about edges) for the triangle group (2, 3, 7), which is the group generated by ….. A convenient fundamental domain for N is the circular arc (non-Euclidean) 14-gon Delta shown in Fig. 1. It will be noticed that t appears as the unshaded triangle immediately below and to the right of P0. There are 168 unshaded triangles, which are the images of t under Gamma168 in Delta and 168 shaded triangles, which are the images of t under anticonformal elements of (2, 3, 7)'. ….
Dalej jest ta Fig. 1. Oto ona, była dla mnie obrazkiem pomagającym intuicji zrozumieć raczej formalne instrukcje geometryczno-algebraiczne:
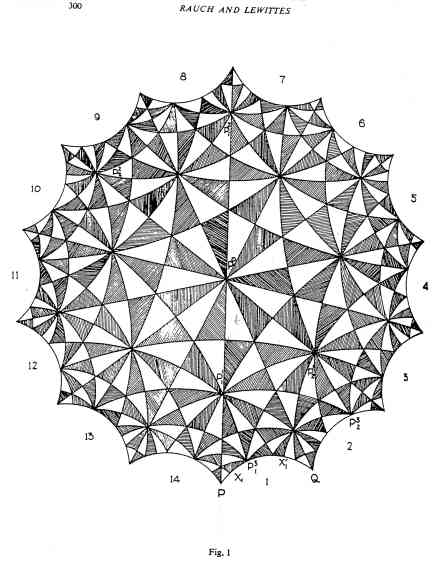
Nie będę ukrywał, że zrozumienie o co chodzi, opanowanie odpowiedniego kawałka algebry i geometrii, przeniesienie idei ze szczebla abstrakcji do szczebla zaprogramowania komputera, zajęło mi dobre parę dni (Laura twierdzi, że cały tydzień nad tym siedziałem, dla mnie to było „mgnienie oka”). Oczywiście były wzloty i upadki, wykrzykiwanie „Eureka” i odwoływanie Eureki. Tak czy siak, w końcu wypociłem. Oto więc moja własna siódemka i moje własne 168 trójkątów:

Komu to potrzebne? Do czego? Ciekawe pytanie. Rożnym ludziom ewidentnie jest to potrzebne na różne potrzeby. Większości zaś nie potrzebne do niczego.
Teraz parę słów wyjaśnienia. Ta figura zajmuje tylko część dysku Poincarego. Nie dochodzi do brzegu:
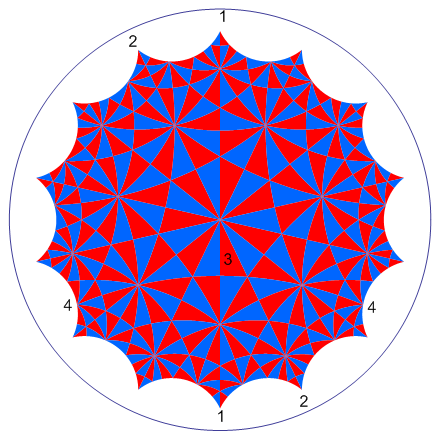
Boki trójkątów są „proste” w geometrii dysku. Przypomnę, że „prostymi” (geodezyjnymi) są tu łuki okręgów, które spotykają się pod katem prostym z obwodem dysku – okręgiem o promieniu równym 1. Wszystkie trójkąty są równoboczne (choć nie równoramienne), wszystkie mają to samo pole powierzchni - te duże i te małe (oczywiście w geometrii dysku), te same kąty.
Zaczyna się konstrukcję od wyliczenia trójkąta 3. Narysowanie prostych (1,1) i (2,2) nie przedstawia trudności. Dalej wszakże trzeba wyliczyć parametry łuku (4,4), a ma być taki, by, zgodnie z instrukcjami, przecinał prostą (2,2) pod katem Pi/3. Dalej trzeba już stosować formuły geometrii hiperbolicznej na odbijanie trójkątów względem swoich boków, bo wszystkie kolejne trójkąty powstają z trójkąta wyjściowego przez kolejne odbicia względem swoich boków. Trzeba już tylko wiedzieć kiedy się zatrzymać, jeśli się bowiem nie zatrzymamy, to zamiast grafiki ilustrującej kwartykę Kleina otrzymamy taką oto mozaikę w stylu Eschera:

A tak naprawdę ciekawe rzeczy zaczynają się dziać dopiero w wyższych wymiarach, gdy brzegiem nie jest po prostu okrąg, tylko rozwarstwiona rozmaitość, a nasza czterowymiarowa czasoprzestrzeń (życie takie, jakie znamy) jest tylko jedną z kilku warstw (Kasjopeańskich „gęstości”?) tego brzegu, brzegu o warstwach różnej wymiarowości, różnej geometrii i o różnych rodzajach „życia”. Teraz powiązać to wszystko z Burkhartem Heimem! Fantazja? Science-Fiction? Utopia? Brednie? Marzenia młodego Wertera? Nie taki on znów młody! Ale głupi, bo niepotrzebnie się zdradza!
P.S. A do zajęcia się kwartyką (powierzchnia czwartego stopnia) Kleina zainspirowało mnie seminarium, jakiego wysłuchałem miesiąc temu:
Philippe Carbonne
(University of Toulouse Le Mirail and Paul Sabatier )
„Autour de la quartique de Klein”
Podobny bbrazek, wzięty z „Notices of the American Mathematical Society” pokazywałem już w październiku 2008 , nie wiedziałem jednak wtedy jeszcze od której strony to się da ugryźć. Zębów zresztą mi brakowało. A dziś już trochę się nadgryźć udało.
Naukowiec, zainteresowany obrzeżami nauki.
Katalog SEO Katalog Stron
map counter
Życie jest religią.
Nasze życiowe doświadczenia odzwierciedlają nasze oddziaływania z Bogiem.
Ludzie śpiący są ludźmi małej wiary gdy idzie o ich oddziaływania ze wszystkim co stworzone.
Niektórzy ludzie sądzą, że świat istnieje dla nich, po to, by go pokonać, zignorować lub zgasić.
Dla tych ludzi świat zgaśnie.
Staną się dokładnie tym co dali życiu.
Staną się jedynie snem w "przeszłości".
Ci co baczą uważnie na obiektywną rzeczywistość wokół siebie, staną się rzeczywistością "Przyszłości"
Lista wszystkich wpisów
Nowości od blogera
Inne tematy w dziale Kultura

