Jako, że Wielkanoc – czas na jaja. Będziemy dziś tłukli eliptyczne jaja ugotowane w poprzedniej notce Wielkopiątkowe kwantowe elipsy. Wychodząc od paczki falowej przedstawionej funkcją:
Ψu,v(x) = (u/π)1/4 exp(-(u+iv)x2/2) , u>0, z=u+iv
doszliśmy do równania:
(u2+v2)x2+ p2+ 2pvx -u = 0.
Przedstawia ona eliptyczne jajo. Ale jajo jest ukryte i trzeba je znaleźć. W Polsce ze zwyczajem szukania ukrytych jaj się nie spotkałem. Nie wiem, może dziś już ten zwyczaj zza oceanu i do nas dotarł? Tak czy siak – poszukajmy.
Mamy u i mamy v. Oba są rzeczywiste. U musi być dodatnie, inaczej nam się paczka rozpadnie. Zrobiliśmy z u,v liczbę zespoloną u+iv. Nikt nas o to nie prosił, ale zrobiliśmy. Na Wielkanoc będzie jak znalazł.
Liczby zespolone z dodatnią częścią rzeczywistą tworzą prawą półpłaszczyznę. Można ją znaleźć w Wikipedii:

Obrazek i nic więcej tam na ten temat nie ma.
Można ją znaleźć u Woframa:
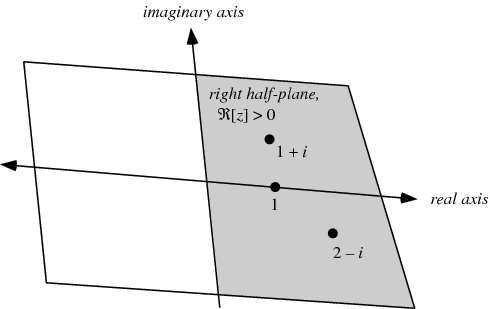
Ten obrazek od Wolframa bardziej nam się podoba, bo zaznaczony jest tam punkt u=1,v=0. To jedynka na osi rzeczywistej. A my jedynkę na osi rzeczywistej lubimy, bo nasze jajowate równanie dla u=1, v=0 staje się równaniem okręgu:
x2+ p2-1 = 0
Okrąg jest ładny, okrągły, zaś punkt u=1,v=0 ciąży po prawej stronie i psuje symetrię. BJAB to zauważył w komentarzu pod poprzednią notką. Ponadto: półpłaszczyzna nic okrągłego w sobie nie ma i coś z tym fantem trzeba w okrągłą wielkanocną niedzielę zrobić. I zrobimy:
Przesuniemy jedynkę do centrum a całą prawą półpłaszczyznę wokół tak przesuniętej jedynki zwiniemy w okrągły dysk. Innymi słowy: zastosujemy wariant transformacji Cayleya.
Wikipedia nam tu jakoś pomóc nie może, ale mamy Google. Po krótkim poszukiwaniu znajdujemy receptę na zwijanie w książce Upmeyera „Jordan Algebras in Analysis, Operator Theory, and Quantum Mechanics, Issue 67”:

Upmeier ma tam transformację z dysku w prawą półpłaszczyznę. Nam potrzebna jest też odwrotna. Niech liczba w prawej półpłaszczyźnie będzie oznaczona jako z, zaś ta na dysku jako w. Upmaier mówi:
z = (1+w)/(1-w)
Stąd, jak komuś nie straszny krótki rachunek, można też, na odwrót, wyrazić w przez z:
w = (z-1)/(z+1)
Jak ktoś się leni, albo nie wierzy, może podstawić do poprzedniego i przekonać się naręcznie, że wyjdzie tożsamość z = z.
Widać teraz, że z=1 przechodzi w w=0, zaś z = 0 przechodzi w w = -1. Że formuła przeprowadza prawą półpłaszczyznę w dysk, tego nie widać – trzeba uwierzyć Cayleyowi, Wikipedii, Upmeierowi, albo trzeba samemu się napracować.
Liczba zespolona w to punkt na dysku. Nasz wyróżniony punkt, z=1, to środek dysku w=0. w to liczba zespolona, punkt wewnątrz dysku. Czemu nie przedstawić jej w formie biegunowej?
w = r exp(iφ )
Teraz
z = (1+r exp(iφ ))/(1-r exp(iφ ))
Co, w razie potrzeby, można rozpisać jako:
z = (1+r cos φ + i r sin φ )/(1 - r cos φ - i r sin φ )
Wracając do naszego równania:
(u2+v2)x2+ p2+ 2pvx -u = 0.
Musimy teraz wyrazić u,v,(u2+v2) prze r i φ i zobaczyć czy nasze równanie się wysymetryzuje czy nie? Jak na razie nic się nie uprościło. I, przez pewien czas, faktycznie, tylko się będzie komplikować. Za to na końcu czeka nas nagroda (tak to już w życiu jest). Ale to już w kolejnej notce.
Naukowiec, zainteresowany obrzeżami nauki.
Katalog SEO Katalog Stron
map counter
Życie jest religią.
Nasze życiowe doświadczenia odzwierciedlają nasze oddziaływania z Bogiem.
Ludzie śpiący są ludźmi małej wiary gdy idzie o ich oddziaływania ze wszystkim co stworzone.
Niektórzy ludzie sądzą, że świat istnieje dla nich, po to, by go pokonać, zignorować lub zgasić.
Dla tych ludzi świat zgaśnie.
Staną się dokładnie tym co dali życiu.
Staną się jedynie snem w "przeszłości".
Ci co baczą uważnie na obiektywną rzeczywistość wokół siebie, staną się rzeczywistością "Przyszłości"
Lista wszystkich wpisów
Nowości od blogera
Inne tematy w dziale Technologie

