Tak pisał śp. ks. prof. Włodzimierz Sedlak w „Na początku było jednak światło”:
„Na początku było... Nie wiadomo co. Na początku może być tylko pasja, jedynie furia poszarpania przesłony, pod którą jest prawda o przyrodzie. Przyrodą jest również owa pasja zrodzona z życia. Prawda jest systemem zamkniętych pól. I to wszystko?
Nie chodzi o to, by inaczej było. Chciałoby się jednym omiotem myśli ogarnąć Wszechświat, Życie i Człowieka. Wyjaśnić to olbrzymie i tajemnicze Trio przyrody, tak harmonijne, tak różne i bliskie jak rytm własnego pulsu, jak niespokojny bieg myślenia i dalekie jak bezmiar.
Na światło stawiam.
Lubię to, co ryzykowne, szalone, z zadatkiem na prawdziwość, choć obłędne. To pasja ścigania przyrody - u jej początków. W fundamentalnych wiązadłach. Może próbę poznawania istoty człowieka już tam trzeba zacząć?”

I ja, śladami Sedlaka, na światło stawiam. I krok po kroku doń zmierzam, choćby i na styk, choćby tylko po asymptocie
„Jak gra, to o najwyższą stawkę. Lepsze to, z ryzykiem złamania karku, niż ustawiczne żucie prawdy. Nawet gdyby cofnięcie problemu do zera wszechegzystencji i wszechrzeczy było osiągalne jak temperatura absolutnego zera - tylko po asymptocie, by nigdy do nich nie dojść. Nawet gdyby prawda o życiu i człowieku była nieskończonością problemową, do której można się po asymptocie mózgiem ślizgać, by nigdy w maksymalny punkt nie trafić, to przecież zawody intelektualne między absolutnym zerem rzeczy i nieskończonością komplikacji życia i człowieczej natury są przepyszną okazją dla rozwinięcia prawdziwego rozmachu poznawania.”
Ciągnę też ku światłu Czytelnika, zachęcam, i przez to zachęcanie i wyjaśnianie sam siebie zachęcam i sam sobie wyjaśniam. I widzę, że to jest dobre.
Póki co nasze światło jest proste, liniowe, wręcz monochromatyczne. Światło to nieskończenie wiele kwantowych oscylatorów. My zajmujemy się jednym. A i ten jeden jedynie obwąchujemy. Lecz tak już być musi. Od czegoś trzeba zacząć, w głębokie i turbulentne wody należy wchodzić ostrożnie, inaczej wiry nas wciągną.
Dziś zatem następny mały kroczek. Mały, maleńki. Tichy prosi o spoiler. Nie tak od razu. Spoiler spoilera to i tak by było za wiele, nie do strawienia.
Wpadło przez okno zespolone z. Wpadło i rozrabia. Zespolone z ma część rzeczywistą i część urojoną. Gdy część urojona jest różna od zera, paczka falowa przestaje mieć minimalną nieoznaczoność mierzoną iloczynem rozmycia pędu i położenia. O tym było w poprzedniej notce Kwantowe bziki.
Dobrze jest zacząć od nieoznaczoności minimalnej, oswoić się z nią, na nieoznaczoność nieminimalną czas przyjdzie potem. Gdy z jest rzeczywiste, nasza paczka falowa z poprzedniej notki ma postać:
ψ0,u(x) = (u/π)1/4 exp(-ux2/2) , u>0.
Gdy u=1, wtedy mamy stan podstawowy oscylatora harmonicznego, kwantową próżnię. Fizycy zapisują często ten wektor jako |0>. Czyli zero kwantów energii. A jednak coś tam się dzieje pomimo zera. I to coś badamy.
W poprzedniej notce badaliśmy z osobna: albo pędy, albo położenia. Dziś zbadamy jednocześnie i dla pędów i dla położeń. Jest do tego narzędzie: transformata Wignera. Ta pozwala na zobrazowanie funkcji od jednej zmiennej przez funkcję od dwóch zmiennych. Transformata Wignera nazywa się czasem „dekwantyzacją”. Pozwala na uzmysłowienie sobie tego jak zjawiska kwantowe „wyglądają” po zrzutowaniu na zwykły klasyczny ekran. Przypomnę ogólną formułę (z Wikipedii):

Zauważmy, że P(x,p) nie czuje stałej fazy funkcji ψ. Ma bowiem w sobie iloczyn ψ i ψ*. Fazy ψ i ψ* się znoszą. Znając P(x,p) możemy odtworzyć ψ jedynie z dokładnością do fazy. Ma to swoje zalety, bowiem na mechanice kwantowej uczymy się, że stała faza funkcji falowej jest nieobserwowalna. Nie znaczy to, że jest niepotrzebna. Przydaje się, i to bardzo, ale, sama w sobie, jest nieobserwowalna.
Podstawiając za ogólne ψ(x) nasze konkretne ψ0,u(x) rozkład P(x,p) daje się wyrachować używając tablic całek. Oto wynik (stałą Plancka ħ kładziemy równą 1):
P(x,p) = (1/π ) exp(- ( ux2+p2/u ) )
Funkcja ta ma stałe wartości gdy stały jest wykładnik: ux2+p2/u = c >0.
Jest to równanie elipsy. Oto konturowe wykresy funkcji P(x,p).
Najpierw dla u=4:

A to dla u=1/4
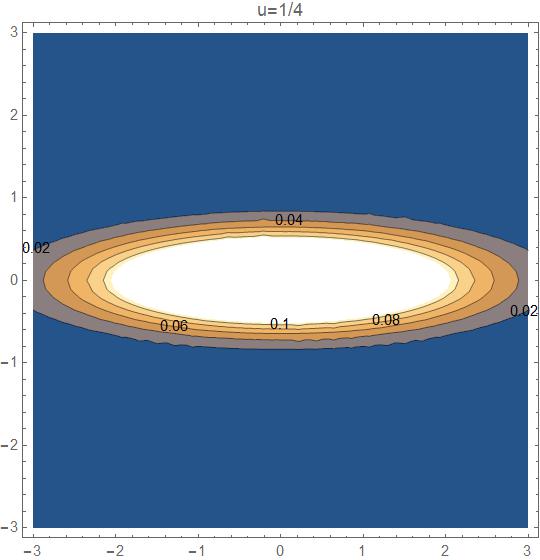
Na osi poziomej położenia x, na osi pionowej pędy p.
A tu już same elipsy opisywane równaniem ux2+p2/u = 1 dla u zmieniającego się od 1/16 do 16 co 15/32:

Dla małych u ściska się rozkład pędów, dla dużych u ściska się rozkład położeń. Półosie naszych elips to a = √ (1/u) , b = √ u. Iloczyn ab = 1. Czyli wszystkie te elipsy mają to samo pole πab=π! Z tego też powodu iloczyn nieoznaczoności pędu i położenia jest ten sam dla każdej z tych elips.
Kiedyś pisałem o parabolach: Parabole. Teraz mamy elipsy. Na razie proste. W następnej notce pozwolimy im się obracać. A dalej, z elips zrobimy geometrię i od razu pojawia się transformacje Lorentza znane z teorii względności. No, może nie tak od razu. Po stycznej....
Naukowiec, zainteresowany obrzeżami nauki.
Katalog SEO Katalog Stron
map counter
Życie jest religią.
Nasze życiowe doświadczenia odzwierciedlają nasze oddziaływania z Bogiem.
Ludzie śpiący są ludźmi małej wiary gdy idzie o ich oddziaływania ze wszystkim co stworzone.
Niektórzy ludzie sądzą, że świat istnieje dla nich, po to, by go pokonać, zignorować lub zgasić.
Dla tych ludzi świat zgaśnie.
Staną się dokładnie tym co dali życiu.
Staną się jedynie snem w "przeszłości".
Ci co baczą uważnie na obiektywną rzeczywistość wokół siebie, staną się rzeczywistością "Przyszłości"
Lista wszystkich wpisów
Nowości od blogera
Inne tematy w dziale Technologie

