Rozkład Wignera i kwantowe upiory

W ostatniej serii natek dyskutowaliśmy klasyczne i kwantowe rozkłady prawdopodobieństwa dla położeń i pędów oscylatora w stanach o określonej energii. Jednak była to dyskusja „albo-albo”. Albo położenia albo pędy. Kwantowy kanon przestrzega przed pomiarami pędu i położenia jednocześnie. Mnie ten kwantowy kanon śmieszy. Pójdzie kiedyś do kosza. Poświęciłem temu cały rozdział w mojej książce. Za jednoczesne pomiary pędu i położenia, co dziś grozi ekskomuniką, będą w niedalekiej przyszłości rozdawać Noble. Ale nie o to mi dziś idzie. Choć w kwantowej teorii, w dzisiejszej jej wersji, pisanie wprost o jednoczesnych pomiarach pędu i położenia jest równie niebezpieczne jak krytyka niektórych posunięć niektórych rządów, niemniej są sposoby by więzienia za taką krytykę uniknąć. Trzeba się tylko odpowiednio ostrożnie wyrażać. I tak też fizycy od dawna robią.

Choć w teorii kwantowej nie ma formuł na jednoczesny, łączny rozkład prawdopodobieństwa dla położenia i pędu, jest jednak „pseudo-rozkład”. Nazywa się to „funkcją Wignera” lub „dystrybucją Wignera”. Formułę można znaleźć w (angielskiej) Wikipedii pod hasłem Wigner quasiprobability distribution.

Gdy funkcja falowa psi jest unormowana, to całka z funkcji Wignera (wzięta w jakimś tam, odpowiednim sensie) daje 1, co sugeruje, co jest (powinno być) jedną z podstawowych własności rozkładu prawdopodobieństwa.

Dla stanów oscylatora harmonicznego o określonej, skwantowanej energii, funkcje Wignera daje się wyliczyć. Same funkcje falowe, jak to widzieliśmy w poprzednich notkach, mają w sobie funkcję eksponencjalną mnożoną przez wielomiany Hermite'a. Ich funkcje Wignera mają funkcję eksponencjalną mnożoną przez wielomiany Laguerre'a. I tu odpowiednią formułę możemy znaleźć w angielskiej Wiki:

Sam tej formuły wyprowadzić nie potrafię, w posiadanych przeze mnie podręcznikach podana jest też bez wyprowadzenia. Zapewne wynika z jakichś tablic całek. Nie mam powodu by tej formule nie ufać. Sprawdziłem dla n=5,6,7 – zgadza się. Zatem prowizorycznie akceptuję dla wszystkich n.

Nasz oscylator jest symetryczny w p i x – tak sobie, dla ułatwienia, przyjąłem. Stąd funkcja Wignera zależy jedynie od p²+x². Gdy się ją maluje, wychodzą kapelusze, takie jak ten: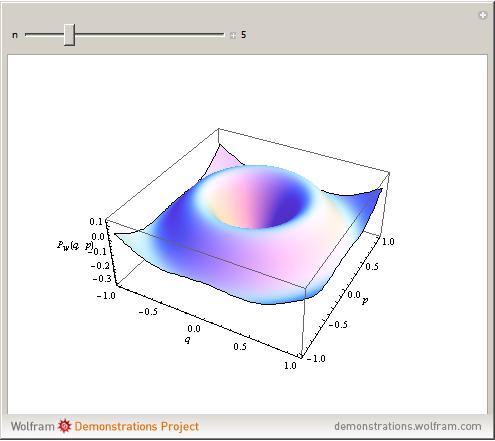

Jednak, ze względu na symetrię, malowanie jej na płaszczyźnie mija się z celem. W dodatku kapelusz może ukrywać pod sobą sprawy niestosowne(nie będę przypominał znanych dowcipów o plaży i kapeluszu). Dlatego wprowadziłem współrzędne biegunowe i namalowałem jedynie zależność od współrzędnej radialnej r. Dodatkowo przeskalowałem, jak w poprzedniej animacji, tak by klasyczny punkt zwrotny był zawsze dla r=1. Wrzuciłem na Youtube.

Co pod osią poziomą – to upiory – ujemne prawdopodobieństwa.