Pod koniec ubiegłego roku zapuściliśmy się w holomorficzne kwantowe lasy. Jednak bez przewodnika tam łatwo pobłądzić. Roślinność tam dziwna, kwiaty, gdy się rozwiną, strzelają w nieskończoność. Choć holomorficzne, jakieś mało pociągające. Co innego w dobrze nam znanych lasach ojczystych, tam grzybów od metra, choćby i czasem niezjadalnych i niemierzalnych.
Rzecz jednak w tym, że te kwantowe holomorficzne lasy są jedynie holograficznymi kodami tych dobrze nam znanych. A hologramy trzeba po prostu umieć odkodowywać. I tym się dziś zajmiemy.
Przypomnę. Holomorficzna przestrzeń Hilberta, oznaczana czasem symbolem HL2(C,m), składa się z super-gładziutkich holomorficznych funkcji F(z), od zmiennej zespolonej z = x+iy, no i takich, które są całkowalne z kwadratem z wagą m, gdzie ( patrz notka Kwantowe integralne niestrawności)
dm(z) = dm = (1/π) exp(-|z|2) dz = (1/π) exp(-(x2+y2)) dx dy
Innymi słowy: jesteśmy w przestrzeni Segala-Bargmanna. Jak stąd przejść do zwykłej przestrzeni Hilberta z podręczników mechaniki kwantowej? Wikipedia nam tu niewiele pomaga. Owszem jest tam rozdział The Segal–Bargmann transform, jest nawet jakby potrzebna nam formuła,

jednak Wikipedia nie jest jasna w tym punkcie i szybko okazuje się, że potrzebna nam jest inna formuła. Tą inną formułę można znaleźć kombinując dwie formuły z pracy Halla o której wspomniałem pod poprzednią notką. Co i zrobiłem. Przejście of funkcji holomorficznych do zwykłych kwantowo-mechanicznych funkcji falowych psi dane jest taką oto formułą całkową:
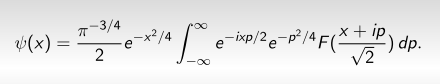
Wygląda bardziej skomplikowanie niż ta elegantka z Wikipedia, ale za to nam pasuje jak ulał. A sprawdzamy to tak: bierzemy funkcje Fn naszej dobrze już znanej bazy ortonormalnej w przestrzeni HL2(C,m):
Fn(z) = zn/√(n!), n=0,1,2,...
no i używając naszej formuły całkowej znajdujemy odpowiednie funkcje ψ n(x). Do liczenia całek dobrze jest użyć jakiegoś programu. Ja używam programu Mathematica. Oto wyniki:
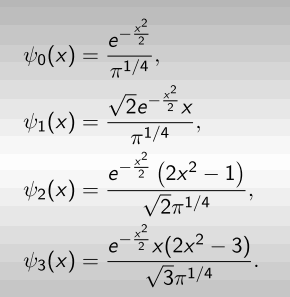
Sprawdzamy, czy jesteśmy w zgodzie z resztą ludzkości. Idziemy na stronę
Quantum Harmonic Oscillator: Wavefunctions i widzimy, że mamy to samo co ma reszta ludzkości – pod warunkiem, że uświadomimy sobie, że nasze x jest bezwymiarowe, czyli nasze x to ichnie y. No i nasze funkcje falowe są też bezwymiarowe. By dodać im wymiary fizyczne trzeba pomanipulować troszkę stałymi: masą oscylatora, jego częstotliwością, no i stałą Plancka. Na razie tym się nie będziemy przejmować. Sam fakt bycia w jednej grupie z resztą ludzkości daje nam poczucie bezpieczeństwa.
Pod wyżej wskazanym linkiem można też znaleźć wykresiki funkcji i ich kwadratów.

Zauważmy, że nasze funkcje, a reprezentują one po kolei podstawowy i kolejne stany wzbudzone oscylatora, są wszystkie rzeczywiste. Bieg czasu będzie tylko zmieniał ich globalną fazę, nic więcej.
Chciałoby się jednak zrozumieć co znaczą te górki i pagórki? Tym się dalej zajmiemy.
Naukowiec, zainteresowany obrzeżami nauki.
Katalog SEO Katalog Stron
map counter
Życie jest religią.
Nasze życiowe doświadczenia odzwierciedlają nasze oddziaływania z Bogiem.
Ludzie śpiący są ludźmi małej wiary gdy idzie o ich oddziaływania ze wszystkim co stworzone.
Niektórzy ludzie sądzą, że świat istnieje dla nich, po to, by go pokonać, zignorować lub zgasić.
Dla tych ludzi świat zgaśnie.
Staną się dokładnie tym co dali życiu.
Staną się jedynie snem w "przeszłości".
Ci co baczą uważnie na obiektywną rzeczywistość wokół siebie, staną się rzeczywistością "Przyszłości"
Lista wszystkich wpisów
Nowości od blogera
Inne tematy w dziale Technologie

