W mechanice klasycznej stan cząstki w danej chwili opisujemy przez określenie pędu p i położenia q. Gdy znamy siły, wtedy możemy stąd wyliczyć pęd i położenie w każdej innej chwili. Pojęciowo jest to proste i w zasadzie do przyjęcia. Podobnie ze światłem, które możemy rozłożyć na harminiczne drgania oscylatorów.
Wiemy jednak, że jest coś takiego jak stała Plancka, że jest coś takiego jak „relacje nieoznaczoności” Heisenberga, że jest coś takiego jak „komplementarność”, że stała Plancka wydaje się nakładać ograniczenia no to co możemy wiedzieć, że gdy chcemy dokładnie poznać położenie, wtedy zaburzamy pęd, a jak chcemy poznać pęd, to zaburzamy położenie. Niby jesteśmy wolni, ale ta nasza wolność ma swoje granice. Obraz ściśle deterministyczny jesteśmy zmuszeni zamienić na obraz deterministyczno-statystyczny.
W klasycznej mechanice statystycznej stan cząstki opisujemy przez rozkład prawdopodobieństwa na przestrzeni fazowej. Miast ostrych pików, punktów (q,p), mamy tam górki i pagórki. Lecz wciąż nie ma ograniczenia na ostrość krajobrazu.
Przychodzi mechanika kwantowa ze swymi operatorami Q i P i cały ten obraz się gubi. Gdy Q i P są przedstawiane jako macierze, krajobraz w ogóle się gubi. Gdy P i Q przedstawiamy jako operatory mnożenia i różniczkowania funkcji falowych, jak to było w poprzedniej notce, bynajmniej nie staje się o wiele lepiej. Funkcja falowa zależy tylko od położenia, w dodatku przychodzi głupawe utożsamianie funkcji różniących się od siebie na zbiorach miary zero, pętają się brzydkie klasy równoważności, przyplątuje się teoria miary. Obrzydliwe. Fizycy to kupują, bo „to działa”, zatem i brzydactwo trzeba przełknąć. Ale czy naprawdę nie ma lepszego towaru?
Owszem, jest, choć nie tak go łatwo kupić. W kwantowych sklepach przeważa tandeta. Za lepszym towarem trzeba się dobrze naszukać.
Lepszy towar.
Ten lepszy towar powstał nie tak znów dawno. Zaczęło się w roku 1928 od rosyjskiego fizyka, Foka (Anglosasi piszą Fock). Potem, w roku 1960 za to co nadgryzł Fok zabrał się matematyk z Princeton, Bargmann. Zabrał się też Segal. I tak powstała reprezentacja Foka-Bargmanna-Segala. Towar najwyższej klasy, zaspokaja wymagania techniczne i estetyczne najwybredniejszych klientów. Ale, jak powiedziałem, w sklepach trudno go znaleźć. Hurtownie tego nie rozprowadzają.
Co to takiego? Jest „przestrzeń Hilberta”? Jest, owszem, ale jaka piękna!
Zatem, w okresie świątecznym, tym prezentem pod choinkę się zajmiemy.
Najpierw przestrzeń fazowa. Mamy q i p. Pojawia się tu problem z modelowaniem matematycznym. Fizyczne q i p mają różne fizyczne wymiary. W modelowaniu matematycznym powinniśmy używać wielkości bezwymiarowych, inaczej wyrażenia typu „2.0 + q” nie mają sensu. Jak przechodzić od wielkości z wymiarami fizycznymi do wielkości bezwymiarowych? To całe rzemiosło i sztuka. To także mistyka, bo może to zależeć od naszych wyobrażeń kosmologicznych: czy Wszechświat ma skończoną objętość? Czy istnieje „kwant długości”? I tym podobne. W każdym konkretnym przypadku możemy znaleźć takie czy inne metody. Problem, w całej ogólności, dotąd czekający na zrozumienie. Zostawmy to zatem na razie w spokoju. W zastosowaniach i tak rzecz wyjdzie. Założę zatem, że nasze q i p są bezwymiarowe. Nie można zadowolić wszystkich. Trzeba wybierać.
W mechanice kwantowej z niezrozumiałych dotąd do końca powodów występują liczby zespolone. Zespolone wartości mają funkcje falowe i „amplitudy prawdopodobieństwa”. Czemu więc nie pójść na całego i nie wprowadzić struktury zespolonej do przestrzeni fazowej? Czemu nie zebrać q i p w jedną liczbę zespoloną z = q+ip? Tak też zrobimy.
Nasza przestrzeń fazowa staje się więc zbiorem liczb zespolonych. Położenie to część rzeczywista zmiennej z, pęd to część urojona.
Przestrzeń Hilberta
Stany układu kwantowego reprezentujemy przez funkcje ψ(z) o wartościach zespolonych. Ale nie byle jakie funkcje! Przez funkcje analityczne aka holomorficzne aka całkowite. Nasze funkcje powinny więc być różniczkowalne, w sensie zespolonym, w każdym punkcie. Każda taka funkcja jest przekształceniem płaszczyzny zespolonej w siebie. W dodatku nie byle jakim przekształceniem, bo każda funkcja holomorficzna jest przekształceniem konforemnym: zachowuje kąty. Można ją przedstawić jako konforemną deformację płaszczyzny zespolonej, tak jak na tym obrazku wziętym z Wikipedii
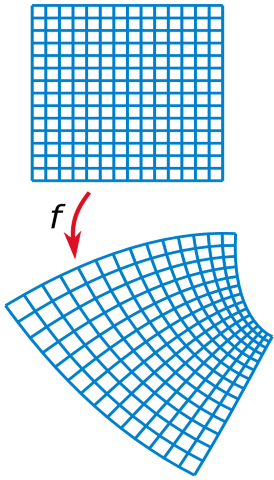
Prostokątna siatka (u góry) wraz z jej obrazem danym względem funkcji holomorficznej f (na dole).
Potrzebna nam jeszcze norma i iloczyn skalarny. To właśnie Bargmann nań wpadł: gaussowski. Z angielskiej Wikipedii:
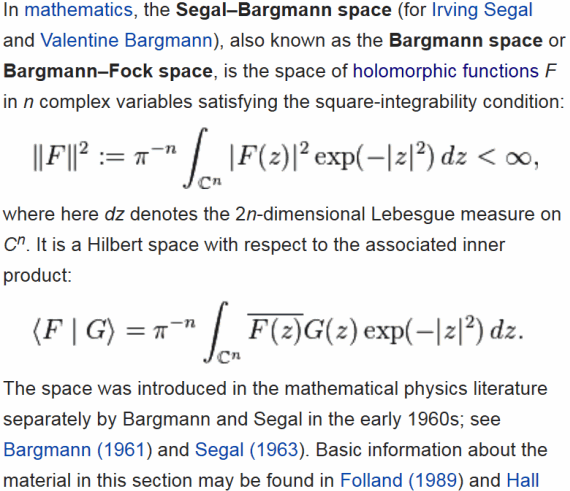
Jak już tego Gaussa przełkniemy (to czynnik eksponencjalny w definicji), wtedy wszystko jest już z górki. Funkcje analityczne o skończonym iloczynie skalarnym tworzą przestrzeń Hilberta. Niczego już nie trzeba „uzupełniać”. Wszystkie nasze funkcje są pięknie gładkie. Żadne zbiory miary zero już nie straszą. Stany kwantowe to piękne, gładkie fale! Ta gładkość może być wielce skomplikowana, tak jak na obrazkach fraktali Mandelbrota:

Czy jednak tego Gaussa w definicji normy łatwo przełknąć? Jedni (Tichy) są z Gaussami za pan brat. Inni będą wybrzydzać, że narusza niezmienniczość względem przesunięć.
Tak czy siak, mamy piękną przestrzeń Hilberta. Teraz już tylko operatory kreacji i anihilacji, operatory Q i P, i dalej w drogę …. koherentną, ku światłu!

W kolejnych notkach ...
A Newdem ilustruje to tak

Naukowiec, zainteresowany obrzeżami nauki.
Katalog SEO Katalog Stron
map counter
Życie jest religią.
Nasze życiowe doświadczenia odzwierciedlają nasze oddziaływania z Bogiem.
Ludzie śpiący są ludźmi małej wiary gdy idzie o ich oddziaływania ze wszystkim co stworzone.
Niektórzy ludzie sądzą, że świat istnieje dla nich, po to, by go pokonać, zignorować lub zgasić.
Dla tych ludzi świat zgaśnie.
Staną się dokładnie tym co dali życiu.
Staną się jedynie snem w "przeszłości".
Ci co baczą uważnie na obiektywną rzeczywistość wokół siebie, staną się rzeczywistością "Przyszłości"
Lista wszystkich wpisów
Nowości od blogera
Inne tematy w dziale Technologie

