Symplektyczne życie w symplektycznych blokach

 

W bloku można mieszkać, do bloku można należeć, można

blokować, choć i można też blogować. Przy tym jedno drugiego

nie wyklucza.

 

Zablokowani w blokach

 

Bloki zresztą bywają różne. W Katowicach ponoć są takie:

 

 

Choć sam tego nie widziałem. W Marsylii jest słynny, nie wiem

dlaczego, „Le Corbusier”

 

 

Z lotu ptaka wygląda tak:

 

 

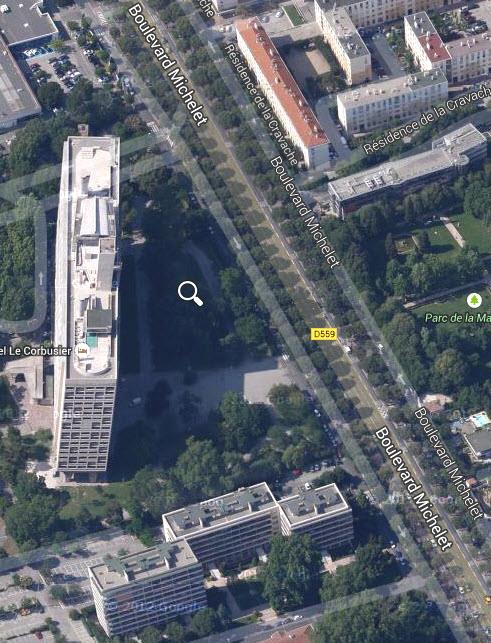
Wspominam o tym, gdyż wielokrotnie będąc w Marsylii co

dzień obok niego, w drodze z CNRS do domu, po bulwarze

Michelet, przechodziłem

 

Będziemy mieć do czynienia z macierzami blokowymi. Polska

Wikipedia nazywa je macierzami klatkowymi. Jeśli o mnie idzie,

to wolę mieszkać w bloku niż w klatce. Pod hasłem „Macierz

klatkowa” dowiemy się, że operacje na macierzach klatkowych

są analogiczne do operacji na zwykłych macierzach. Jednak

formuły na obliczanie wyznacznika macierzy blokowej są

ubogie, zbyt ubogie jak na nasze potrzeby.

 

Udajmy się więc z wizytą do Wikipedii angielskiej. Tam, pod

hasłem „determinant” (wyznacznik) znajdziemy więcej

ciekawych informacji. Przytaczam je bez tłumaczenia.

Matematyka jest językiem uniwersalnym gdzie sensu można

się domyślić z oznaczeń i formuł – w dowolnym języku.

 

 

Spróbujmy zastoswać jedną z tych formuł do wyliczenia

wyznacznika macierzy blokowej J

 

0 I

-I 0

 

jest to standardowa macierz definiująca strukturę

symplektyczną – dyskutowaliśmy to w kilku poprzednich

(symplektycznych) notkach.

Klatki tej macierz są same macierzami nxn, gdzie 0 oznacza

macierz zerową, zaś I oznacza macierz jednostkową.

 

Formuła (1) nam nie pasuje, bowiem w formule tej w lewej

dolnej klatce powinno być zero, a my mamy I. Podobnie nie

pasuje nam formuła następna. Formuła (2) nam nie pasuje,

bowiem zakłada, że lewa górna klatka jest macierzą

odwracalną, zaś my mamy tam 0. Podobnie nie pasuje nam

formuła (2). Natomiast formuła (4) jest jak znalazł. Macierze C i

D u nas są przemienne, bowiem D jest u nas macierzą zerową

– ta jest przemienna z każdą macierzą, podobnie zresztą jak

macierze I i -I. W naszym przypadku AD = 0, BC = -I. Stąd

 

det(J) = det( 0-(-1) ) = det(I) = 1.

 

Grupa symplektyczna

 

Grupa symplektyczna to zbiór macierzy S spełniających

warunek

 

S^TJS = J

 

gdzie „T” oznacza transponowanie macierzy. . Macierze

należące do grupy symplektycznej nazywamy, jak

najnaturalniej, macierzami symplektycznymi.

 

Gdy J jest macierzą 2nx2n, grupę symplektyczną macierzy

zespolonych onaczamy symbolem Sp(2n,C). Gdy interesują

nas wyłącznie macierze rzeczywiste, używamy symbolu

Sp(2n,R). Normalnie, w zastosowaniach do fizyki, interesujemy

się zwykle grupą Sp(2n,R). Jednak nic nam nie przeszkadza w

rozważaniu także grupy Sp(2n,C), czasem takie rozważania

prowadzić mogą do interesujących wniosków.

 

Zapiszemy najpierw nasz warunek na macierz symplektyczną

w postaci blokowej. Niech zatem S będzie macierzą blokową:

 

A B

C D

 

Wtedy macierz S^T ma postać

 

A^T C^T

B^T D^T

 

Zauważmy, że macierze B i C zamieniły się miejscami.

 

Przygotowałem na tablicy mały wykładzik, trochę po polsku,

trochę angielszczyzny.

 

 

 

 

 

Uwaga: w jednym z komentarzy pod notką BJAB słusznie zauważył: "Wydaje mi się, że (na ostatnim slajdzie z dowodem) wniosek, że macierz odwrotna należy do Sp jest przedwczesny. Powinien być po wniosku, że macierz transponowana należy do Sp."

Dowodzę tam, że macierze symplektyczne tworzą grupę.

Najważniejsze są formuły (9)-(11). Z nich będziemy jeszcze

korzystać.

 

Robię to wszystko powoli, po kolei. Nigdy nie wiadomo, może

komuś się do czegoś przyda..... To tak jak z nauką gry na

instrumencie muzycznym. Pewne ćwiczenia są banalnie łatwe,

nudne choć żmudne. Inne stanowią wyzwanie. Gdy przez nie

wreszcie przejdziemy, wtedy możemy sami coś twórczego do

muzyki wnieść.