Fizyka się geometryzuje i algebraizuje. Bóg jest matematykiem. Dążąc do poznania Przyrody jesteśmy na etapie symplektyzacji nauki. O tym było w
poprzedniej notce. Niniejsza notka jest jej kontynuacją.
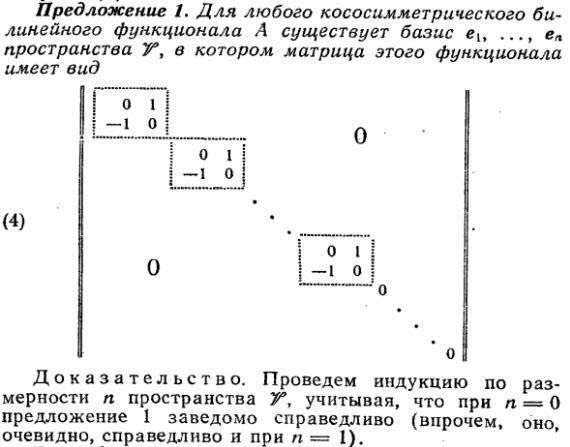
Przyroda dała nam przestrzeń wektorową V a w niej formę antysymetryczną f. Kiedy trochę popracujemy, potrafimy dobrać bazę w V taką, że w tej bazie macierz naszej formy symplektycznej ma postać:
Te zera w prawym dolnym roku gryzą w oczy. Przyroda jest jednak oszczędna. Nie będzie produkować niepotrzebnych zer – tak sobie możemy pomyśleć. Więc i my tych zer się pozbywamy. Odtąd interesują nas jedynie formy niezdegenerowane. Takie formy nazywamy formami symplektycznymi. Dla formy symplektycznej można zawsze dobrać bazę tak, by macierz tej formy miała postać
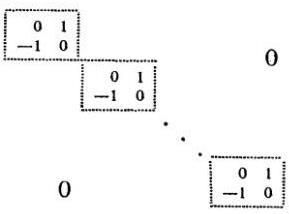
Dobieramy bazę parami (opuszczam zera):
f(e1,e2)=1 f(e2,e1)=-1
f(e3,e4)=1, f(e4,e3)=-1
f(e5,e6)=1, f(e6,e5)=-1
…...
To tak jak na nauce tańca. Partnerzy tańczą w parach.
Można jednak pogrupować wektory bazowe inaczej. Najpierw rząd chłopców, potem rząd dziewcząt, Dwa rzędy, partnerzy naprzeciwko siebie. Tak bywało zresztą w dawnych tańcach salonowych.
Dla formy symplektycznej wymiar przestrzeni V musi być zawsze parzysty: 2n. Nie ma tam siedzących pod ścianami, bez partnerów. Przy ustawieniu bazy: najpierw chłopcy, potem dziewczęta, macierz naszej formy wygląda tak:
f[1,n+1] =1 f[n+1,1]= -1
f[2,n+2]=1, f[n+2,2]=-1
f[3,n+3]=1, f[n+3,3]=-1
…..
f[n,2n]=1, f[2n,n]=-1
Reszta to zera. Bazę, w której nasza forma ma taką właśnie standardową postać nazywamy
bazą symplektyczną. Kopiuję z wykładu
Mechanika Hamiltonowska:

Dowodząc istnienia takiej bazy (w poprzedniej notce), raz po raz dokonywaliśmy swobodnych wyborów. Te wybory mogły się odbywać inaczej. Wtedy i baza wyszłaby inna. Zatem spodziewamy się, że baz symplektycznych jest od metra. Przyroda dała nam formę symplektyczną f, ale bazy nam nie dała. Wybór bazy do nas, do ludzi należy. Po to mamy wolną wolę. Chcielibyśmy wszakże wiedzieć ile tej wolnej woli mamy. Ile dokładnie jest takich baz symplektycznych, jak je sparametryzować? O tym będzie w następnej notce.
----------------------------
Uwaga: Pierwszy sposób ustawiania wektorów bazowych to tak jakby ustawiać (grupować) położenia i pędy parami.
q1,p1,q2,p2,....,qn,pn
Drugi sposób to ustawienie
q1,...,qn,p1,....,pn








Komentarze
Pokaż komentarze (14)