Coś o sferach

Sfery bywają różne. Pisząc „sfera” mam tu na myśli sferę dwu-wymiarową. Oto cała rodzina takich sfer:

 

 

Sferę należy odróżniać od kuli. Kula jest wypełniona w środku. Sfera to powierzchnia kuli. Sfery mogą być materialne – jak bańki mydlane. Te są zawsze niedoskonałe. Są sferami jedynie w przybliżeniu. Doskonałą sferę możemy jednak sobie wyobrazić. Oto przykłady sfer z wyobraźni:

(Z notki Nie bójta się … liczb zespolonych )

 

 

 

Jeszcze doskonalsza od sfery z wyobraźni jest sfera matematyczna. Sfera o środku w punkcie o współrzędnych (x0,y0,z0) i promieniu R opisywana jest równaniem

 

(x – x0)² + (y - y0)² + (z-z0)² = R²

 

Oczywiście środek sfery nie jest punktem sfery. Jest punktem we wnętrzu sfery.

 

Jeśli środek sfery umieścimy w początku kartezjańskiego układu współrzędnych (x0 = y0 = z0 = 0) i jeśli, dla prostoty, wybierzemy promień równy jedności (w jakichś tam, wygodnych dla danego celu jednostkach), wtedy równanie sfery przybiera prostszą postać:

 

x² +y² + z² = 1

 

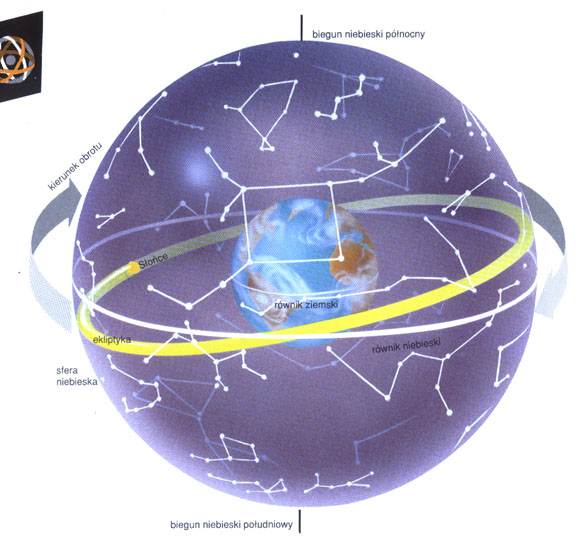
Ta nazywa się zwykle „sferą jednostkową”. I tą się zajmiemy. Sferę taką możemy przeciąć płaszczyzną z=0 i zrzutować na tę płaszczyznę świecąc laserem umieszczonym na północnym biegunie sfery:

 

 

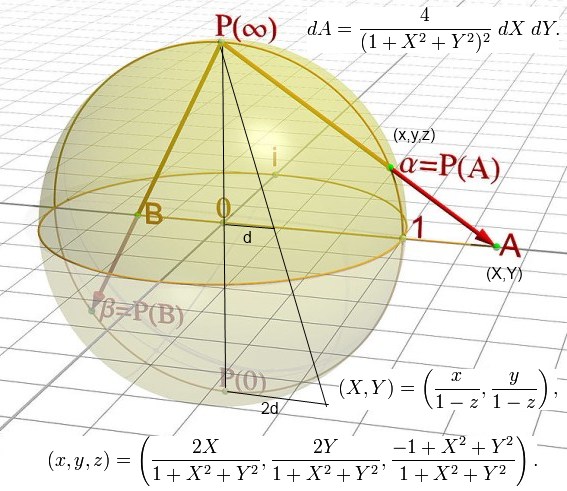
To rzut stereograficzny z poprzedniej notki. Promień wychodzący z bieguna północnego i uderzający w płaszczyznę w punkcie A przechodzi przez powierzchnię sfery w punkcie P(A). Promień łączący biegun północny z B trafia w sferę w punkcie P(B). I tak możemy każdy punkt sfery przedstawić jako punkt na płaskiej mapie. No, „prawie każdy”. Bowiem czym bliżej bieguna północnego tym dalej nasz promień lasera musi sięgać by przeciąć się z płaszczyzną. Obraz samego bieguna północnego ucieka do nieskończoności. Przejścia pomiędzy współrzędnymi (x,y,z) punktu P(A) na sferze spełniającymi równanie

 

x² +y² + z² = 1

 

i punktem A na płaszczyźnie o współrzędnych (X,Y) dane są prostymi formułami rzutu stereograficznego

 

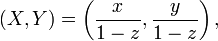
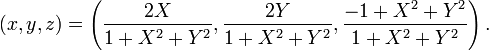
Można je znaleźć w angielskiej Wikipedii. Polska Wikipedia jeszcze się ich nie doczekała.

 

Rzut stereograficzny ma ciekawą własność: zachowuje kąty. Jeśli na powierzchni sfery dwie drogi przecinają się pod jakimś kątem, wtedy i na płaskiej mapie przecinają się pod tym samym kątem. Mapa stereograficzna zniekształca odległości, zniekształca pola powierzchni, ale jest wierna gdy idzie o kąty. Przekształcenia zachowujące kąty nazywamy zwykle przekształceniami konforemnymi. Rzut stereograficzny jest przykładem takiego przekształcenia. W angielskiej Wikipedii możemy też znaleźć formułę na zniekształcanie pól powierzchni:

 

 

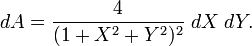
Jeśli weźmiemy maleńki (infinitesimalny) kwadracik na płaszczyźnie o bokach dX,dY i środku (lub rogu) w punkcie o współrzędnych (X,Y), wtedy odpowiada on (nieco krzywemu) kwadracikowi na powierzchni sfery, ale o polu powierzchni dXdY pomnożonym przez 4/(1+X²+Y²)².

 

Spróbujmy zrozumieć skąd się bierze ta czwórka w mianowniku. Rozważmy okolice punktu X=0,Y=0. Te odpowiadają okolicom bieguna południowego sfery. Biegun południowy sfery leży w płaszczyźnie z = -1. Zatem odległość od bieguna północnego do południowego jest dwa razy większą niż odległość od bieguna północnego do płaszczyzny na którą rzutujemy. Promień lasera wychodzący z bieguna północnego i przechodzący w pobliżu punktu X=Y=0 będzie odbywał zatem dwa razy dłuższą drogę na płaszczyźnie z = -1, gdzie leży biegun południowy. I to w każdym kierunku. Skoro tak, to mały kwadracik w okolicach X=Y=0 na płaszczyźnie z=0 będzie miał dwa razy dłuższe boki na płaszczyźnie z = -1. Zaś 2x2 = 4. Uwiarygodniliśmy więc czwórkę!

 

Oczywiście nikt nam nie każe umieszczać naszego oświetlającego lasera na biegunie północnym. Kogo w ogóle biegun północny interesuje? Nasza mapa zniekształca najmniej elementy sfery położone po przeciwnej stronie. Tam po prostu dwa razy rozciąga równomiernie we wszystkich kierunkach. Jeśli więc chcemy by okolice Warszawy były w centrum mapy i w miarę nie zniekształcone, wtedy umieścimy punkt z którego rzutujemy po przeciwnej stronie kuli ziemskiej. Gdzie to wypadnie? Gdzieś na oceanie? Czy może trafi przypadkiem na ląd?

 

Tak czy siak warto obejrzeć śliczny filmik na Youtube pokazujący jak zmienia się obraz stereograficzny gdy zmieniamy punkt z którego świecimy laserem.

 

P.S. Chciałem przejść w tej notce od przestrzeni do czasoprzestrzeni, ale notka się jakoś sama rozrosła. Zatem czasoprzestrzeń musi poczekać.

 

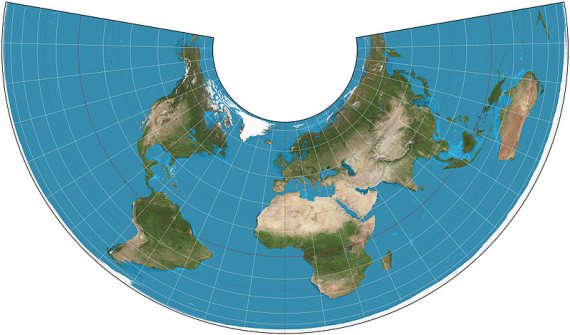
P.S.2 Na koniec: istnieje całe mnóstwo różnych rzutowań (patrz np. Melita Kennedy, Understanding Map Projections, pdf 1.7 MB) używanych w kartografii. Każde z nich ma swoje dodatnie i swoje ujemne strony. Oto przykład mapy na której zachowane są wiernie stosunki pól powierzchni, ale za to kąty (i także odległości) są zniekształcane: