Dobrze jest znać sfery. Zarówno te niskie jak i te wysokie. Dobrze też znać płaszczyzny. I dobrze umieć schodzić ze sfery na płaszczyznę i wspinać się z płaszczyzny na sferę. Pomoże nam w tym astronomia, trochę matematyki, a i o fizykę się przy tym otrzemy.
Rzecz sprowadza się do języka którym się porozumiewamy. Rzecz ludzka, że chcemy być zrozumiałymi dla innych. Gdy chcemy komuś wytłumaczyć gdzie coś jest, odnosimy to do punktów w miarę stałych. Posługujemy się często takimi czy innymi mapami. Na mapach mamy współrzędne. To samo dotyczy map gwiezdnych. By mówić o współrzędnych trzeba się zgodzić co do układu współrzędnych. Mógłbym wybrać układ współrzędnych, że oś z jest nad moją głową, oś x przede mną, oś , oś y czy to po lewej czy to po prawej ręce. Taki układ wędrowałby ze mną i przewracał się, gdy kładę się podłodze. Niezbyt to wygodne. Szukamy więc czegoś bardziej stałego – podobnie jak to jest z miłością. Szukają też czegoś bardziej stałego astronomowie. Pomaga nam w tym znajomość faktów – faktami, ich gromadzeniem, systematyzacją, analizą, prawidłowościami zajmowali się ciekawi przyrody ludzie od zarania dziejów. Co dziś wiemy?
Słońce wydaje się mieć nieco większą masę niż Ziemia, zatem wygodnie jest myśleć, że to Ziemia obraca się po orbicie względem Słońca. Inne planety Układu Słonecznego mają swe orbity w mniej więcej tej samej płaszczyźnie – nazywamy ją płaszczyzną ekliptyki. Ziemia ma swą oś, i nie jest ta oś prostopadła do płaszczyzny ekliptyki. Prostopadły do osi Ziemi jest „Równik Świata”. Ta ziemska oś w miarę porządnie utrzymuje swój kierunek – jak to mają w swoim zwyczaju żyroskopy. Czemu tak jest? To zagadka. Można się oczywiście powoływać na prawa mechaniki Newtona, ale te prawa są zagadką. Czemu takie a nie inne? Kto za nie opowiada? Kto może je zmienić?
Na diagramie wygląda to tak:
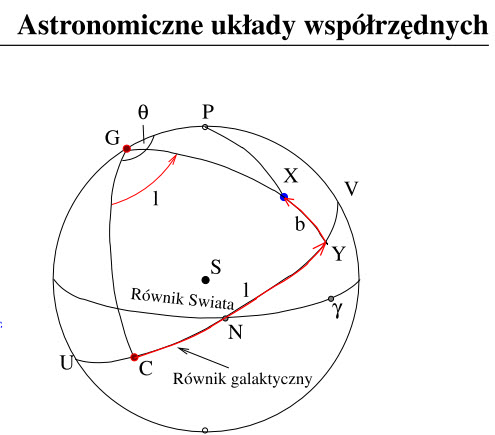
Punkt P to okolice Gwiazdy Polarnej. Oś Ziemi nie zawsze, jak się wydaje, była zwrócona w tę stronę. Jest coś takiego jak „precesja”. Punkt G to Północny Biegun Galaktyczny. Na kolorowej mapie nieba, miast na biało-czarnym diagramie wygląda to tak:
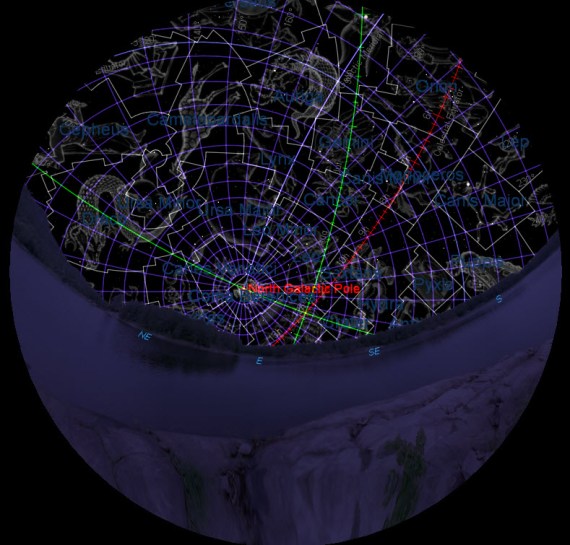
Próbowałem umiejscowić ten Biegun Galaktyczny dokładniej. Wyszło coś takiego:

Gdzieś w okolicach Bereniki:
Warkocz Bereniki (łac. Coma Berenices, dop. Comae Berenices, skrót Com) – gwiazdozbiór nieba północnego, wydzielony z dwóch innych przez Tycho de Brahe na początku XVII w. Nazwany na cześć Bereniki, królowej Egiptu i żony Ptolemeusza, która przyrzekła złożyć swoje długie włosy w ofierze, jeśli jej mąż powróci zwycięsko z wojennej wyprawy do Azji. Po szczęśliwym powrocie Berenika dotrzymała obietnicy i ofiarowała włosy świątyni w Zephyrium, jednak następnego dnia bogowie przenieśli je do gwiazd.
W gwiazdozbiorze znajduje się Biegun Galaktyczny – punkt leżący o 90° na północ od równika galaktycznego (zob. współrzędne galaktyczne), M64 (Galaktyka Czarnooka), M53 oraz Gromada Coma (Melotte 111).
Jest to rejon najdalej położony od Drogi Mlecznej.
Najjaśniejsze gwiazdy:
β Comae Berenices – 4,23m
α Com Diadem – 4,32m
γ Comae Berenices – 4,35m
Możemy więc oś z naszego układu ustawić w kierunku Bieguna Galaktycznego (północnego), oś x w kierunku punktu równonocy wiosennej – to jeden z dwóch punktów w których Równik Galaktyczny przecina się z Równikiem Świata, oś y prostopadle do tych dwóch – no i mamy układ współrzędnych na którym, mniej więcej, możemy polegać.
Punkt na sferze niebieskiej można wtedy określić przy pomocy dwóch kątów: lambda i beta (na diagramie oznaczonych literkami l i b. Lambda zmienia się od 0 do 2 pi (0 do 360 stopni). Beta zmienia się od -pi/2 do pi/2 (-90 do +90 stopni).
Mając kąty lambda i beta punktu na sferze niebieskiej możemy znaleźć współrzędne kartezjańskie jednostkowego wektora skierowanego w tym kierunku:
x = cos λ cos β
y = sin λ cos β
z = sin β
Z prawa Pitagorasa i z tożsamości trygonometrycznych wnioskujemy, że kwadrat długości wektora (x,y,z) jest jedynką:
x2 + y2 + z2 = 1.
No i dobrze.
Możemy się więc posługiwać albo kątami, albo współrzędnymi x,y,z. Ale: kąty są potrzebne tylko dwa, zaś współrzędne potrzebne są trzy. Za to muszą spełniać warunek unormowania: x2 + y2 + z2 = 1. Trochę to niewygodne. Na pomoc przychodzi rzut stereograficzny. Ten występuje w kilku odmianach, Wybierzmy tę przedstawioną na obrazku z angielskiej Wikipedii:
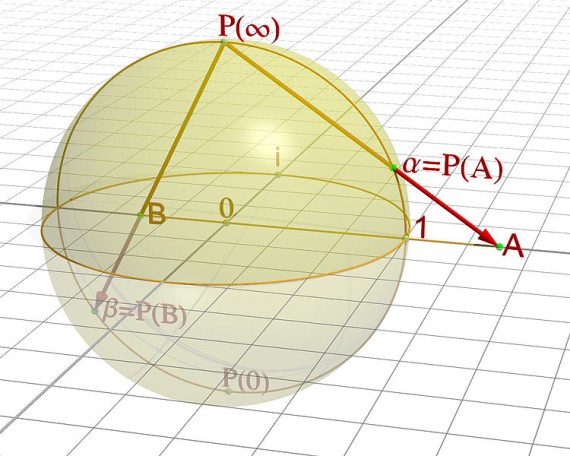
Półkula południowa jest teraz przedstawiana przez punkty we wnętrzu koła o promieniu 1, półkula północna przez punkty na zewnątrz tego koła, równik to to koło (na płaszczyźnie z=0). We współrzędnych, jeśli przez X,Y oznaczymy współrzędne rzutu stereograficznego:
X = x/(1-z)
Y = y/(1-z)
Można też przejść na odwrót, od współrzędnych X,Y na płaszczyźnie do współrzędnych x,y,z w przestrzeni. Formuła jest taka:
x = 2X/(1+X2+Y2)
y = 2Y/(1+X2+Y2)
z = (-1+X2+Y2)/(1+X2+Y2)
Jeśli wprowadzimy teraz liczbę zespoloną
Z = X+iY
to oto mamy: każdej gwieździe na niebie możemy przyporządkować liczbę zespoloną!
„Tylko po co?” – może słusznie ktoś zapytać. Otóż dokonując transformacji na liczbach zespolonych, na przykład
Z --> (aZ+b)/(cZ+d)
możemy przesuwać gwiazdy! I to relatywistycznie!!! Jaką moc nam to daje!!!
Ale o tym w kolejnych notkach.
P.S. W czasie moich studiów na kierunku fizyka teoretyczna egzamin z astonomii przeszedłem z wielkim trudem. Mogłem więc w tej notce popełnić jakieś błędy. Mam nadzieję, że uważni Czytelnicy je zauważą i mnie poprawią - gdy zajdzie taka potrzeba.
Naukowiec, zainteresowany obrzeżami nauki.
Katalog SEO Katalog Stron
map counter
Życie jest religią.
Nasze życiowe doświadczenia odzwierciedlają nasze oddziaływania z Bogiem.
Ludzie śpiący są ludźmi małej wiary gdy idzie o ich oddziaływania ze wszystkim co stworzone.
Niektórzy ludzie sądzą, że świat istnieje dla nich, po to, by go pokonać, zignorować lub zgasić.
Dla tych ludzi świat zgaśnie.
Staną się dokładnie tym co dali życiu.
Staną się jedynie snem w "przeszłości".
Ci co baczą uważnie na obiektywną rzeczywistość wokół siebie, staną się rzeczywistością "Przyszłości"
Lista wszystkich wpisów
Nowości od blogera
Inne tematy w dziale Technologie

