Mondrian 168

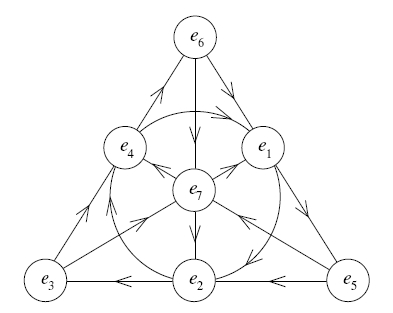
W poprzedniej notce liczyliśmy symetrie najprostszej płaszczyzny rzutowej, płaszczyzny Fano, tej o siedmiu tylko punktach i siedmiu tylko liniach. A każda linia leży na trzech punktach, a każdy punkt leży na trzech liniach. I każde dwie linie się przecinają w jednym punkcie. Święta doprawdy jest ta geometria?

 

 

Licząc symetrie („automorfizmy”) doliczyliśmy się liczby 168 = 7x6x4. Maxima – program komputerowy – wyprodukowała nam 168 zero-jedynkowych macierzy 3x3. Te tworzą grupę. Mnożąc przez siebie dwie spośród tych 168 macierzy otrzymujemy trzecią macierz – też jedną z tych 168. Biorąc odwrotność jednej z tych 168 macierzy otrzymujemy (na ogół inną) macierz z tej naszej 168-elementowej grupy.

 

Grupa ta, a matematycy mają dla niej symbol GL(3,2) lub SL(3,2) lub PSL(3,2), żyje sobie swoim własnym życiem. Geometria sama jest jakoś tam zakodowana w strukturze tej grupy symetrii. Symetrie, symetrie, symetrie – w nich jest wszystko – trzeba tylko umieć czytać. Uświadomił nam to Felix Klein – patrz <a href='http://pl.wikipedia.org/wiki/Dzia%C5%82anie_grupy_na_zbiorze' _fcksavedurl='http://pl.wikipedia.org/wiki/Dzia%C5%82anie_grupy_na_zbiorze' _fcksavedurl='http://pl.wikipedia.org/wiki/Dzia%C5%82anie_grupy_na_zbiorze' _fcksavedurl='http://pl.wikipedia.org/wiki/Dzia%C5%82anie_grupy_na_zbiorze'>Działanie grupy na zbiorze</a> w Wikipedii, i tam m.in:

 

Działanie grupy – w algebrze i geometrii sposób opisania symetrii obiektów za pomocą pojęcia grupy. Istotne elementy obiektu opisane są za pomocą zbioru, a jego symetrie za pomocą jego grupy symetrii, która składa się z wzajemnie jednoznacznych przekształceń geometrycznych wspomnianego zbioru. Wówczas grupę tę nazywa się także grupą permutacji (szczególnie, jeśli zbiór jest skończony lub nie jest przestrzenią liniową) lub grupą przekształceń (szczególnie, gdy zbiór jest przestrzenią liniową, a grupa działa jak przekształcenia liniowe zbioru).

 

Działanie grupy jest elastycznym uogólnieniem pojęcia grupy symetrii, w której każdy jej element „działa” jak wzajemnie jednoznaczne przekształcenie (lub „symetria”) pewnego zbioru, lecz bez utożsamiania tego elementu ze wspomnianym przekształceniem. Pozwala to bardziej wyczerpująco opisać symetrie obiektu, takiego jak wielościan, przez zadziałanie tej samej grupy na kilku różnych zbiorach, np. zbiorze wierzchołków, zbiorze krawędzi i zbiorze ścian wielościanu.

 

Niezmienniczość działania grup na obiektach geometrycznych była główną ideą tzw. programu erlangeńskiego Feliksa Kleina. Ewaryst Galois w swoich pracach dotyczących rozwiązywania wielomianów przez pierwiastniki badał działanie grup Galois na zbiorach pierwiastków wielomianu.

 

Umożliwiając stosowanie idei geometrycznych do bardziej abstrakcyjnych tworów działania grup dostarczają wysokiego poziomu abstrakcji. Wiele obiektów matematycznych ma naturalnie określone na sobie działanie grupy. W szczególności grupy mogą działać także na innych grupach, a nawet na samych sobie.

 

A my mamy grupę złożoną ze 168 elementów. Czy 168 to nie za duża liczba na jak na nasze głowy? Klasa złożona ze 168 uczniów i uczennic to byłoby istotnie dużo jak na głowę nauczyciela. Ale państwo ma może mieć 50 milionów obywateli i jednak jakoś, z trudem bo z trudem, daje się nim rządzić. Więc nie bójmy się liczby 168, mnożenia i odwracania.

Czy naszą grupę można jakoś namalować? Choćby i wyszedł nam abstrakcyjny obrazek, jednak co obrazek to obrazek.

 

Więc, proponuję, zabawmy się w malowankę naszej grupy. Użyję do tego celu powszechnie dostępnego programu Maxima, programu, który już przedstawiałem w poprzednich notkach.

 

Uprzedzam z góry, że nasz obrazek grupy będzie zawierał elementy subiektywne, ale każde dzieło prawdziwie artystyczne takie elementy zawiera.

 

Przypomnę najpierw programik w języku Maxima z poprzedniej notki:

 

(%i1) p1:[0,0,1]$
p2:[0,1,0]$
p3:[0,1,1]$
p4:[1,0,0]$
p5:[1,0,1]$
p6:[1,1,0]$
p7:[1,1,1]$
(%i8) p:[p1,p2,p3,p4,p5,p6,p7]$
(%i9) grm:[]$
(%i10) block([l,tmp],

grm:[],
l:0,

for i:1 thru 7 do

for j:1 thru 7 do
(if is(notequal(p[j],p[i]))then

for k:1 thru 7 do
(if
is(notequal(k,i)) and is(notequal(k,j)) and is(notequal(p[k],mod(p[i]+p[j],2)))
then

(l:l+1, tmp:[p[i],p[j],p[k]], grm:append(grm,[matrix(tmp[1],tmp[2],tmp[3])])))),

print(l));

Po wykonaniu tego programu mamy macierze naszej grupy ustawione w tablicy grm o 168 elementach. Chcemy teraz utworzyć tabelkę mnożenia (składania symetrii) naszej grupy. Biorąc macierz z adresem i, mnożąc ją prze macierz z adresem j otrzymamy inną macierz z naszej tablicy, z pewnym określonym adresem, oznaczmy go przez m(i,j). W ten sposób otrzymamy tabelkę o 168 wierszach i 168 kolumnach, a w każdej klatce naszej tabelki będzie stała określona liczba, od 1 do 168 – adres wyniku mnożenia i-tej macierzy prze j-tą.

 

Poprośmy Maximę by nam tę tabliczkę mnożenia wyrachowała. Ale nie każmy jej wypisywać na ekranie, bo się tam nie zmieści!

 

for i:1 thru 168 do
block(print("Obliczam wiersz ",i),
for j:1 thru 168 do
for k:1 thru 168 do
(if is(equal(mod(grm[i].grm[j],2),grm[k])) then (m[i,j]:k,return)));

 

Niby każę Maximie zawiadamiać mnie obliczeniu kolejnego wiersza, ale ta jakoś sobie te obliczenia optymalizuje i zawiadamia mnie po obliczeniu 63 wierszy. A cały ten rachunek trwa na moim PC około 5 minut. Zapewne można to usprawnić i skrócić, ale tu zdaję się na specjalistów od programowania i upraszczania – ja z trudem piszę program, który działa bez błędów … i idę dalej.

 

Mamy więc tabelkę mnożenia naszej grupy symetrii. Może się przydać. Spróbujmy ją namalować. W kwadracie 168x168 będziemy kolorować klatki kolorem zależnym od numeru iloczynu odpowiednich elementów grupy. W tym celu ładujemy do Maximy pakiet draw:

 

load(draw)$

 

Dalej, ściągamy sobie pakiet qdraw.mac i umieszczamy go w folderze w którym zainstalowana jest Maxima:

 

\Maxima-5.27.0\share\maxima\5.27.0\share\graphs

 

No i malujemy:

 

qdensity(float(m[ceiling(i),ceiling(j)]),[i,1,168,1],[j,1,168,1],palette(color));

 

Dodałem tu funkcje „float” i „ceiling”, bo zdaje się, że pakiet qdraw oczekuje liczb typu „float”, a nasza tabelka m[i,j] oczekuje z kolei liczb całkowitych jako argumentów.

 

Otrzymujemy taki oto obrazek naszej grupy symetrii:

 

 

Widać coś w rodzaju okresu 7.

 

Mondrian to to jeszcze nie jest:

 

Piet Mondrian, właściwie Pieter Cornelis Mondriaan (ur. 7 marca 1872 w Amersfoort, Holandia, zm. 1 lutego 1944 w Nowym Jorku, Stany Zjednoczone) – malarz holenderski. Współzałożyciel grupy De Stijl (1917), twórca neoplastycyzmu, jednego z najwcześniejszych kierunków postulujących w malarstwie abstrakcję geometryczną. Operował prostymi, poziomymi i pionowymi liniami, prostokątami i kolorami podstawowymi, np. w "Kompozycji z czerwienią, żółcieniem i błękitem" (1921). Wywarł wpływ na rozwój abstrakcji w malarstwie i na architekturę XX w.

 

 

 

Możemy jednak nieco popracować nad paletą kolorów – i nasze dziełko może iść na wystawę i do muzeum!

 

Tak więc mamy jakiś obraz naszej grupy. W kolejnej notce będę kontynuował analizę artystyczną tego tworu.