Masa fotonu i prawo Coulomba czyli co ma piernik do wiatraka

Piszę chętnie o obrzeżach nauki, czasem wypływam nawet niebezpiecznie daleko od brzegu na burzliwe fale morza wątpliwych hipotez. Czasem wzlatuję ponad poziomy i szybuję wraz z ptakami wysoko w niebieskich przestworzach narażony na wichry i turbulencje. Mój dom jest jednak na lądzie, dobrze zakotwiczony w solidnym granicie. Do tego domu trzeba od czasu do czasu wrócić – zejść z nieba na ziemię – choćby po to by nie zapomnieć skąd się wywodzę.

Trochę przypadkiem a trochę nieprzypadkowo padło w jednym z komentarzy do poprzedniej notki pytanie:

Prawo Coulomba mówi, że siła wzajemnego oddziaływania dwóch punktowych ładunków elektrycznych jest wprost proporcjonalna do iloczynu tych ładunków i odwrotnie proporcjonalna do kwadratu odległości między nimi.

To prawo jest niemalże identyczne jak prawo kwadratów. Czyli oddziaływania grawitacyjnego, określenie grawitacja podmieniono tu iloczynu ładunku.

Co ma wspólnego Coulomb z masą,?

Podczas gdy jednostronne apodyktyczne deklaracje komentatorów typu „jest tak a tak” często ignoruję, na pytania jednak staram się odpowiadać. Pytanie jest konkretne a odpowiedź na nie wymaga osobnej notki – stąd też dzisiejszy, trochę nadprogramowy, choć wciąż w temacie, wpis.

Rzecz dotyczy fizyki. Fizyka jest nauką ścisłą. Według Wikipedii, która od czasami, raczej przez przypadek, stwierdza prawdę:

Nauki ścisłe to inaczej nauki matematyczne i przyrodnicze, czyli grupa nauk, które zajmują się badaniem otaczającego świata oraz konstruowaniem abstrakcyjnych modeli, mogących służyć do tego opisu.

Nauki ścisłe to:

* Matematyka

* Fizyka

* Chemia

* Biologia

* Informatyka

* Geografia fizyczna

* Astronomia

Wspólną cechą nauk ścisłych jest stosowanie matematyki jako metody opisu i modelowania zjawisk oraz weryfikowanie hipotez za pomocą doświadczeń lub dowodów matematycznych. Do opracowywania danych doświadczalnych stosowana jest statystyka (dział matematyki).

By odpowiedzieć ściśle, jak przystało na fizyka, nie mogę zatem obyć się bez matematyki – ta bowiem jest podstawą modelowania, przewidywania i sprawdzania przewidywań. Matematyka jednak odstrasza, bowiem stopień przygotowania matematycznego Czytelników jest bardzo różny. Co zatem robić? Dać za wygraną? To niesportowo. Jest inne wyjście: oddać przynajmniej smak ścisłości. Wtedy, gdy ktoś zasmakuje, będzie chciał smacznego więcej. A smaczne potrawy można się nauczyć sporządzać samemu, nie trzeba chodzić do wykwintnych restauracji i polegać na ekspertach-kucharzach.

Powróćmy więc do problemy masy i prawa odwrotnych kwadratów. Prawo odwrotnych kwadratów występuje zarówno gdy idzie o przyciąganie grawitacyjne jak i elektrostatyczne. Czym dalej jest planeta od Słońca, tym słabiej Słońce na planetę działa, tym słabsza jest przyciągająca siła grawitacji. Dwa razy dalej – cztery razy słabiej. Trzy razy dalej – dziewięć razy słabiej. Dziesięć razy dalej – sto razy słabiej. Siła przyciągania F jest odwrotnie proporcjonalna do kwadratu odległości:

F = k/r²

gdzie k jest współczynnikiem proporcjonalności, stałym dla danych ciał i dla danego ośrodka.

Dokładnie takie samo prawo rządzi wzajemnym przyciąganiem (różnoimiennych) ładunków elektrycznych. Badał to Coulomb i stąd nazwa – prawo Coulomba.

W fizyce dążymy jednak do tego by od praw szczegółowych przechodzić do praw ogólnych, z których prawa szczegółowe wynikają, których są konsekwencjami. Chcemy jakby odczytać „kod podstawowy Przyrody”, Słowo, które „było na początku”. W przypadku prawa Coulomba chcemy zrozumieć skąd się ono bierze? Dlaczego prawo kwadratów a nie np. prawo sześcianów? Zadawał sobie takie pytanie Newton, zadawał sobie takie pytanie Maxwell. Dziś wiemy jak można prawo Coulomba wyprowadzić z praw jak nam się wydaje bardziej fundamentalnych, bardziej ogólnych, o większym zakresie zastosowań. Potrzebna jest jednak do tego znajomość rachunku różniczkowego a z tą bywa kiepsko. Pozostaje mi zatem oddanie smaku tych ogólniejszych praw.

Wszyscy chyba znamy pojęcia energii kinetycznej i energii potencjalnej. Interesuje nas tutaj przede wszystkim energia potencjalna. Czym wyżej uniesiemy nad ziemię kamień tym więcej może narobić szkód przy spadnięciu – tym większa jest jego energia potencjalna. Jakby w samej przestrzeni była zakodowana jakaś informacja – bowiem dla samego kamienia co za różnica czy jest tu czy gdzie indziej?

Tak powstało pojęcie potencjału pola grawitacyjnego i pola elektrycznego:

„Potencjałem pola grawitacyjnego w danym punkcie nazywamy stosunek energii potencjalnej, jaką ma w tym punkcie umieszczone tam ciała, do masy tego ciała.”

Dla prostoty oznaczę ten potencjał literką u. W prostych szkolnych tekstach znajdziemy:

W polu jednorodnym wzór ma postać:

u = gh

Ale pole grawitacyjne Ziemi nie jest polem jednorodnym. Jest jednorodne jedynie w przybliżeniu. Przecież przyciąganie ma kierunek „ku środkowi planety” a te kierunki się zbiegają, nie są równoległe. Formuła nie przybliżona a ścisła to

u = -GM/r

Tutaj G jest stałą grawitacyjną, M – masą przyciągającego ciała. Dla grawitacji mamy więc dwie formuły:

Formułę na siłę:

F = -GMm/r²

u = -GM/r

Formuła na potencjał wydaje się być bardziej podstawową, bowiem nie występuje w niej masa m przyciąganego ciała. Jest jedynie masa M – źródła pola grawitacyjnego, źródła potencjału.

Z jednej formuły łatwo przejść do drugiej. Z formuły na siłę przez „całkowanie” po drodze, do formuły na potencjał, z formuły na potencjał, przez „różniczkowanie”, do formuły na siłę. Szczegóły nie są teraz istotne. Istotne jest to:

Formuła na potencjał wydaje się być bardziej podstawową, bowiem nie występuje w niej masa m przyciąganego ciała. Jest jedynie masa M – źródła pola grawitacyjnego, źródła potencjału.

Wynika stąd między innymi i to: pole grawitacyjne nie jest polem sił! Jest polem potencjału!

Wiem o tym, że będą ludzie gorąco protestujący – ale co zrobić. Bez protestów byłoby nudno.

Skąd jednak ta formuła:

u = -GM/r

Czy można ją wyprowadzić z jakiegoś bardziej podstawowego prawa? A co, jeśli Ziemia zamiast być prawie kulą będzie miała kształt ziemniaka, jak niektóre asteroidy?

Asteroid Eros. Częściowo widoczny krater – na pograniczu dnia i nocy – ma średnice 5.3 km.

Czy wtedy też będzie obowiązywała ta sama formuła? A jak będzie w tunelu we wnętrzu Ziemi? Jeśli tunel będzie wiódł do samego środka Ziemi, to jasne, że w samy środku nie będzie działała na „spadające ciało” żadna siła. Tymczasem ze wzoru

F = -GMm/r²

wynikałoby, że w środku Ziemi, przy r=0, powinna działać siła nieskończona! Zatem powyższe formuły na siłę i na potencjał nie są podstawowymi. Musi istnieć formuła podstawowa, dobra zarówno blisko jak i daleko, dobra przy każdym kształcie, na zewnątrz i wewnątrz źródła pola grawitacyjnego. I podobnie dla pola elektrostatycznego. Co to za formuła?

I znów niepodobna się obejść bez rachunku różniczkowego – przedstawię zatem jedynie smak.

Odpowiedzią jest równanie różniczkowe Poissona:

W Wiki czytamy:

Równanie różniczkowe Poissona - niejednorodne równanie różniczkowe cząstkowe liniowe drugiego rzędu typu eliptycznego.

Równanie to zapisać można w postaci:

lub inaczej

Funkcję f zmiennych przestrzennych traktuje się jako znaną.

Równanie można również zapisać explicite dla przestrzeni o zadanym wymiarze.

Dla przestrzeni trójwymiarowej przyjmuje ono postać:

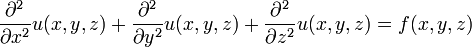
Poisson 3

Pomijając współczynnik proporcjonalności, funkcja f występująca po prawej stronie to gęstość masy źródła dla grawitacji i gęstość ładunku elektrycznego źródła dla pola grawitacyjnego. Fizycy i matematycy potrafią równanie Poissona rozwiązywać. Dajcie nam rozkład gęstości źródła, bez względu na to jaki źródło ma kształt i jak jest masa czy ładunek we wnętrzu źródła rozłożona – wyliczymy potencjał w każdym punkcie – zarówno na zewnątrz jak i we wnętrzu źródła! A nasze wyliczenia można sprawdzić w doświadczeniu! Faktycznie, przez całe już setki lat wyliczano i sprawdzono – i widzieli fizycy, że to było dobre. I tak się równanie Poissona nobilitowało – stało się jednym z podstawowych równań fizyki.

Dla źródła w kształcie idealnej kuli w istocie otrzymujemy rozwiązanie u=k/r – jak należało tego oczekiwać. A wewnątrz kuli inaczej u = kr – i znika paradoks nieskończonej siły we wnętrzu Ziemi!

Wszystko byłoby pieknie-ładnie, gdyby nie Einstein i jego szczególna teorii względności. Fizycy szybko odkryli, że równanie Poissona nie jest „relatywistycznie niezmiennicze”. W teorii względności czas i przestrzeń zbierają się jakoś w całość – w czasoprzestrzeń. W równaniu Poissona występuje przestrzeń, o czasie się nie mówi. Można czas wstawić do niego „na pałę”, ale wstawianie na pałę nie zawsze pomaga. Trzeba więc było wrócić do Maxwell, popatrzeć co ten miał do powiedzenia i spróbować zmałpować stamtąd, bowiem równania Maxwella legły u samych podstaw idei Einsteina.

W drugim tomie jego dzieła, wydanie z roku 1873, znajdujemy następujące formuły:

Rzecz dotyczy co prawda rozchodzenia się światła i fal elektromagnetycznych, ale co za różnica? Jest zmodyfikowany Poisson? Jest! Na następnej stronie Maxwell wyjaśnia:

Zamiast Kmu można więc podstawić 1/c2, gdzie c jest prędkością rozchodzenia się światła w próżni. W ten sposób otrzymujemy kandydata na „ulepszone równanie Poissona” - zgodne z wymaganiami szczególnej teorii względności, „relatywistycznie niezmiennicze”. To nazywa się niejednorodnym równaniem falowym d'Alemberta. Znów możemy sięgnąć do nieodzownej Wikipedii, która zapisze to równanie w postaci

Drugą i trzecią linijką nie należy się przejmować. Nasza Wikipedia wpuszcza nas tu w maliny – w tym przypadku wprowadza naiwnych ludzi w błąd, bowiem równanie to jedna rzecz a warunki początkowe dla tego równania to rzecz zupełnie inna – zadajemy je zależnie od zagadnienia jakie mamy rozwiązać!

W równaniu Poissona był symbol trójkąta – trzy wierzchołki przypominają nam o trzech „pochodnych” - po x, po y, po z – trzy osie w przestrzeni. W równaniu d'Alemberta mamy także pochodną po czasie – czas to czwarta oś w czasoprzestrzeni. Fizycy wymyślili więc znaczek dla tej operacji – kwadracik z czterema wierzchołkami – nazywa się to „dalambercjan” lub operator d'Alemberta:

lub

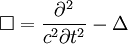
dalambercjan 2

Ale to jeszcze nie wszystko. Oprócz teorii względności mamy wszakże mechanikę kwantową. Najpierw był de Broglie wiążący z materią „fale materii”, potem Schrodinger, który napisał równanie jakie te fale materii winny spełniać, aż wreszcie pojawiło się relatywistyczne równanie falowe znane dziś jako równanie Kleina-Gordona:

W równaniu tym wciąż jeszcze brak prawej strony – gdzie mielibyśmy zadany rozkład gęstości źródeł. Nie musimy się jednak tym przejmować – zawsze możemy po prawej stronie równania zamiast 0 napisać h(x,y,z,t) i myśleć, że jest to właśnie gęstość „źródła”. Troche mi niewygodnie pisać kwadraciki, zatem zamiast symbolu kwadracika będę pisał „*d*d”.Wraz z prawą stroną nasze już teraz relatywistyczne równanie opisujące rozchodzenie się fal materii dla cząstek o niezerowej masie spoczynkowej m₀– uogólnienie równania Poissona – wygląda tak:

(*d*d + m₀²c²/h² )u = h

Proste, nieprawdaż? U – to pole potencjału, h – to gęstość źródła. Tutaj stała Plancka winna być ta z kreseczką, pamiętajmy o tym.

Chcemy teraz to równanie rozwiązać, by przekonać się jak będzie wyglądało pole potencjału wokół spoczywającego ładunku czy spoczywającej masy. I są na to sposoby. Nasza polska Wikipedia jeszcze tak daleko nie zaszła, musimy się więc podeprzeć angielską lub francuską. Przede wszystkim interesuje nas rozwiązanie statyczne – gdy nic się nie zmienia w czasie. Wtedy zamiast kwadracika możemy użyć trójkąta. Interesuje nas też rozwiązanie z symetria obrotową – bo zakładamy sobie, że Ziemia czy co tam jest źródłem pola – jest okrągła. W ten sposób trafiamy na stronę w angielskiej Wiki:

Screened Poisson equation

Równanie tam rozważane nosi nazwę: „Ekranowane równanie Poissona”. Mamy tam stałą lambda, dla nas jak znalazł. Zakładając, dla prostoty, że nas obiekt – źródło pola, ma zaniedbywalne rozmiary, jest „punktowy”, znajdujemy rozwiązanie :

Nie przejmujmy się tym, że teraz pojawiła się literka G zamiast u. W naszym przypadku idzie o to samo. Za stałą λ wiemy co mamy podstawić:

λ = m₀c/h

Nazywa się to „potencjałem Yukawy.

Uwaga: Jak ktoś ciekaw – może poczytać o potencjale Yukawy i siłach jądrowycha także zobaczyć wykresy różnych potencjałów używanych w fizyce jądrowej

No to wróćmy do fotonu. Jeśli przyjmiemy, że foton jest „bezmasowy”, czylim₀=0,wtedymamy e⁰=1, i otrzymujemy

u(r) = k /r

gdzie k jest stałą, zależną od źródła. Jest to właśnie „prawo kwadratów”, „potencjał Coulomba”. Jeśli jednak foton ma masę spoczynkową różna od zera, wtedy pojawia się, przed 1/r, człon tłumiący

e^-^lambda ^r

Czym większa masa – tym silniejsze tłumienie.

A tak wygląda wykres potencjału Yukawy V_y, w porównaniu z potencjałem Coulomba V_g – ten obrazek zwinąłem z dokumentu „Das Phänomen Schwerkraft: Von Newtons fallendem Apfel zu Schwarzen Löchern” - Zjawisko ciążenia: od spadajacego jabłaka Newtona do czarnych dziur

To tłumienie, odchyłkę od prawa Coulomba, widać dopiero na dużych odległościach. Jak dużych? Jeśli wierzyć fizykom, to masa spoczynkowa fotonu, jeśli jest różna od zera, musi być mniejsza niż 1/100000000000000000 eV. Prędkość światła to 300000000 m/s.

Stała Plancka ma wartość

h=6.58211899×10⁻¹⁶ eV.s

Obliczając zatem m₀c/h otrzymamy – jeśli się gdzieś w obliczeniach nie pomyliłem

197,464,000 m

Na takiej odległości dopiero będzie w istotny sposób zauważalne odchylenie od prawa Coulomba dla pola elektrycznego. Pojawi się „efekt ekranowania”. No, wyczuje się to odchylenie nawet na odległościach kilka razy mniejszych.

I w istocie, choć rzecz dotyczy grawitacji a nie elektromagnetyzmu, fizycy próbują wyjaśnić anomalne zachowanie się amerykańskiej sondy kosmicznej Pioneer właśnie przez odchylenie od prawa Coulomba z użyciem potencjału Yukawy. Tak jakby „sama przestrzeń” tłumiła Coulombowskie oddziaływanie grawitacyjne, jakby grawitacja ulegała „zmęczeniu” przy pokonywaniu dużych odległości. Jakby światło ulegało zmęczeniu, czy też się „starzało”. A wszystko to zawarte jest w formule na potencjał Yukawy!

Powróćmy zatem do wyjściowego pytania: Co ma wspólnego Coulomb z masą?

Odpowiedź na to pytanie zawarta jest we wzorze na potencjał Yukawy. Czym większa byłaby masa spoczynkowa fotonu, tym większe i łatwiej zauważalne odchylenie od prawa Coulomba. Tym większe tłumienie.

Potencjał Yukawy stosują fizycy jądrowy gdy opisują oddziaływanie nukleonów (protonów i neutronów) poprzez wymianę mezonów pi - pionów. Pion ma stosunkowo dużą masę ~100 MeV, stąd tłumienie sił jądrowych następuje bardzo szybko – nie sięgają poza jądro.

Uwaga: Masywne fotony poruszałyby się z prędkościami mniejszymi od c a pole elektryczne opisywane byłoby potencjałem Yukawy. A co by było gdyby fotony czy inne „gluony” poruszały się z prędkością większą od c? Można i na pytanie spróbować odpowiedzieć. Trzeba w naszym równaniu wziąć m₀ urojone, zamiast m₀ podstawić im0. Wtedy miast tłumienia pojawią się oscylacje. Będziemy mieli dwa niezależne rozwiązania:

V(r) = sin(m₀c r/h)/r

lub

V(r) = cos(m₀c r/h)/r

Ich wykresy wyglądają (w jednostkach m₀c/h)jakoś tak:

Przypomina to nieco potencjały u Boscovicha. Tyle, że strefy przyciągania i odpychania zmieniają się ściśle periodycznie. Wkraczamy w dziedzinę fantastyki naukowej.

Oczywiście by dojść do tych wszystkich wniosków musiałem pójść na skróty – oddać raczej smak (choć jestem pewien, niektórzy Czytelnicy nazwą to niesmakiem) niż ściśle wyprowadzać krok po kroku.

Podsumowanie: Potencjał Coulomba (prawo kwadratów) można otrzymać rozwiązując niejednorodne równanie Poissona. Od równania Poissona można przejść do równania falowego i do równania Kleina-Gordona. To ostatnie opisuje oddziaływania poprzez oddziaływania gluonów masywnych i prowadzi do potencjału Yukawy. Potencjał Yukawy mówi nam jak modyfikuje się prawo Coulomba gdy gluony (np. Fotony) są masywne.