Foton zakręcony

Nie jestem pewien czy ta wiedza kursuje wśród ludu, ale fotony są zawsze zakręcone. Czy to w lewo czy w prawo, czy to w superpozycji lewego i prawego zakręcenia, ale gdyby foton w tym swoim kręcie zatrzymać - przestałby być fotonem. Tak jak orzeł: gdyby mu odjąć skrzydła, nie byłby już orłem. To tyle tytułem poetyckiego wstępu.

Zacznę od fragmentu moich zapisków (którymi, nota bene,  ostatnio dzieliłem się z pomagającą mi w rachunkach Kleopatrą). Oto ten fragment.

Fatalne jest tu użycie przeze mnie angielskiego terminu "helicity". Po polsku nazywa się to "skrętność" (ewentualnie wiralność, ale ta się kojarzy z wirusem).

Więc jest coś takiego jak operator skrętności. Na co on działa? Na funkcje falowe, albo, jak kto woli, na wektory stanu (tak to fizycy nazywają). A co to są te funkcje falowe? Sprawa prosta. Kurs mechaniki kwantowej zwykle zaczyna się od równania Schrodingera. Tam występuje funkcja falowa Ψ(x) (gdzie x to położenie) lub Ψ(p)  (gdy wygodnie nam pracować w przestrzeni pędów). Przejście od Ψ(x) do Ψ(p) ( i na odwrót) dane jest przez transformatę Fouriera, znaną wszystkim matematykom, fizykom i inżynierom. Nam będzie łatwiej pracować w reprezentacji pędowej, czyli z funkcjami falowymi zależnymi od p. Taka jest specyfika fotonów. Fizycy o tym wiedzą, i ja o tym wiem (jestem na pół fizykiem).

Dalej jest bezmasowe neutrino, inaczej zwane neutrinem Weyla . Tam funkcja falowa to kolumienka dwóch funkcji zespolonych

 Ψ1(p)
 Ψ2(p)

A fotonów się tak łatwo nie daje opisać. Są komplikacje przy porodzie. Bierzemy kolumienkę trzech funkcji zespolonych

Ψ1(p)
Ψ2(p)
Ψ3(p)

ale ta kolumienka rodzi zrośnięte bliźniaki i trzeba potem chirurgicznie foton oddzielić. Lancet używany do tej chirurgii to operator skrętności Lambda zdefiniowany powyżej.

Dla każdego niezerowego p Lambda(p) to 3x3 macierz hermitowska. Ma trzy wartości własne i trzy prostopadłe do siebie wektory własne. Możemy je z łatwością znaleźć przy pomocy programu np. Reduce czy Mathematica. Reduce zachowuje się tu w miarę rozsądnie, podczas gdy Mathematica dostaje czkawki i trzeba ją po plecach klepać by się nie zakrztusiła na śmierć.

Tak wygląda nasza macierz Lambda zakodowana dla programu Mathematica:

lambdaf = {{0, -I*p3/((p1^2 + p2^2 + p3^2)^(1/2)),
   I*p2/((p1^2 + p2^2 + p3^2)^(1/2))}, {I*
    p3/((p1^2 + p2^2 + p3^2)^(1/2)),
   0, -I*p1/((p1^2 + p2^2 + p3^2)^(1/2))}, {-I*
    p2/((p1^2 + p2^2 + p3^2)^(1/2)),
   I*p1/((p1^2 + p2^2 + p3^2)^(1/2)), 0}}

MatrixForm[lambdaf]

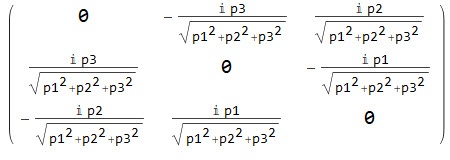
Obliczamy wartości własne i wychodzą 0,1,-1, tyle, że w nieco dziwnej formie:

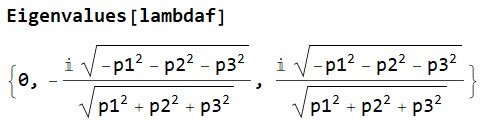
Znajdujemy odpowiednie wektory własne

i ustawiamy je w kolumienki

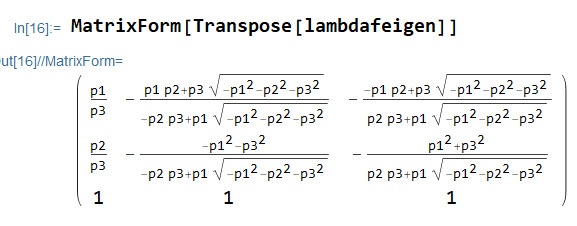
Program Reduce (liczyła Kleopatra) wypluwa sensowniejsze wzory:

I teraz normując każdą z kolumienek do 1 i przestawiając je otrzymujemy unitarną macierz W1 z poprzedniej notki.

Kolumny 2 i 3 powyżej opisują stany fotonu spolaryzowanego kołowo, o skrętności +1 i -1 (prawo i lewo skrętnie). Kolumna pierwsza (druga w W1) opisuje stany cząstki bezmasowej o spinie zero. Trudno te stany zgrabnie wyciąć. To tak jak ze wstęgą Mobiusa. Niby jest dwuwymiarowa, ale na płaszczyźnie nie da się jej rozpiąć, trzeba ją zanurzać w trzech wymiarach. Fotonom potrzebne są tylko dwa stany polaryzacji, ale trzeba je zanurzać w przestrzeń o większej liczbie wymiarów. Fakt życia. Zajmiemy sie tym dokładniej w kolejnych notkach.