Jak to już tradycyjnie jest w mechanice kwantowej, stany kubita reprezentowane są przez wektory o długości/normie 1 w dwuwymiarowej zespolonej przestrzeni Hilberta C2. Dwuwymiarowa przestrzeń zespolona C2 jest czterowymiarową przestrzenią rzeczywistą R4, a warunek noma = 1 jest równaniem 3-wymiarowej sfery S3 w tej czterowymiarowej przestrzeni. Pisałem o tym w notce Kubitiowa 3-sfera. Sparametryzowaliśmy tę sferę trzema kątami:
X = sin (φ/2) cos ( ψ)
Y = sin (φ/2) sin ( ψ)
Z= cos (φ/2) cos ( θ+ψ)
W = cos (φ/2) sin ( θ+ψ)
Przy tym
0 ≤ φ ≤ π, 0 ≤ θ,ψ ≤ 2π
Idzie teraz o to jak tę sferę można/należy sobie wyobrazić? Jak ją przedstawić graficznie? Sferę dwuwymiarową, na przykład powierzchnię Ziemi, zwykle przedstawiamy na dwuwymiarowej płaszczyźnie przy użyciu takiej czy innej siatki kartograficznej . Można też użyć rzutu stereograficznego. I tak postąpimy w naszym przypadku. Zrzutujemy sferę S3 na R3 stereograficznie, z punktu X=Y=Z=0, W=1 na przestrzeń x,y,z rozumianą jako X,Y,Z przy W=0. By zrozumieć jak to się robi, można zajrzeć do Wikipedii pod hasło 3-sphere. Formuły są proste:
x = X/(1-W)
y = Y/(1-W)
z = Z/(1-W)
Punkt W=1, z którego rzutujemy ucieka do nieskończności. Punkt pod nim, W=-1, przechodzi w x=y=z=0. Dla punktów na równiku W=0, mamy x=X,y=Y,z=Z.
Chcemy teraz zobrazować linie współrzędnych kątowych φ,ψ,θ przez równania parametryczne
x(φ,ψ,θ ) = sin (φ/2) cos ( ψ) / (1-cos (φ/2) sin ( θ+ψ))
y(φ,ψ,θ ) = sin (φ/2) sin ( ψ) / (1-cos (φ/2) sin ( θ+ψ))
z(φ,ψ,θ ) = cos (φ/2) cos ( θ+ψ) / (1-cos (φ/2) sin ( θ+ψ))
Potrzebny nam do tego program rysujący parametryczne powierzchnie. Kiedyś, przed laty, taki program polecałem. Dziś ten dawny program (oparty na Javie) nie chce juz działać. Próbowałem wymieniony w notce o kubitowej 3-sferze program MathMod, ale też nie udało mi się nic nim namalować. Próbowałem programu Octave - też bez rezultatu. Może ktoś z czytelników coś znajdzie - mi się nie udało. Zatem opiszę jak to robię przy użyciu komercyjnego programu Mathematica. Nie znalazłem innego rozwiązania.
Najpierw wprowadzam parametryzację sfery S3:
X[theta_, phi_, psi_] = Sin[phi/2]*Cos[psi]
Y[theta_, phi_, psi_] = Sin[phi/2]*Sin[psi]
Z[theta_, phi_, psi_] = Cos[phi/2]*Cos[psi + theta]
W[theta_, phi_, psi_] = Cos[phi/2]*Sin[psi + theta]
Rysuję parametrycznie trzy powierzcnie kątów theta i psi przy ustalonym phi równym kolejno Pi/4, Pi/2, 3 Pi/4:
p1 = ParametricPlot3D[{X[theta, Pi/4, psi]/(1 - W[theta, Pi/4, psi]),
Y[theta, Pi/4, psi]/(1 - W[theta, Pi/4, psi]),
Z[theta, Pi/4, psi]/(1 - W[theta, Pi/4, psi])}, {psi, 0,
2 Pi}, {theta, 0, 2 Pi},
PlotRange -> {{-2.5, 2.5}, {-2.5, 2.5}, {-1.3, 1.3}},
Mesh -> {0, 20}, PlotStyle -> {Orange, Specularity[White, 10]},
PlotPoints -> 50]
p2 = ParametricPlot3D[{X[theta, Pi/2, psi]/(1 - W[theta, Pi/2, psi]),
Y[theta, Pi/2, psi]/(1 - W[theta, Pi/2, psi]),
Z[theta, Pi/2, psi]/(1 - W[theta, Pi/2, psi])}, {psi, 0,
3 Pi/2}, {theta, 0, 2 Pi},
PlotRange -> {{-2.5, 2.5}, {-2.5, 2.5}, {-1.3, 1.3}},
Mesh -> {0, 20}, PlotStyle -> {Orange, Specularity[White, 10]},
PlotPoints -> 50]
p3 = ParametricPlot3D[{X[theta, 3 Pi/4,
psi]/(1 - W[theta, 3 Pi/4, psi]),
Y[theta, 3 Pi/4, psi]/(1 - W[theta, 3 Pi/4, psi]),
Z[theta, 3 Pi/4, psi]/(1 - W[theta, 3 Pi/4, psi])}, {psi, 0,
2 Pi}, {theta, 0, 2 Pi},
PlotRange -> {{-2.5, 2.5}, {-2.5, 2.5}, {-1.3, 1.3}},
Mesh -> {0, 20}, PlotStyle -> {Orange, Specularity[White, 10]},
PlotPoints -> 50]
I pokazuję wszystkie trzy powierzchnie razem
q1 = Show[{p1, p2, p3}, Background -> Black]
Powstaje taki obrazek
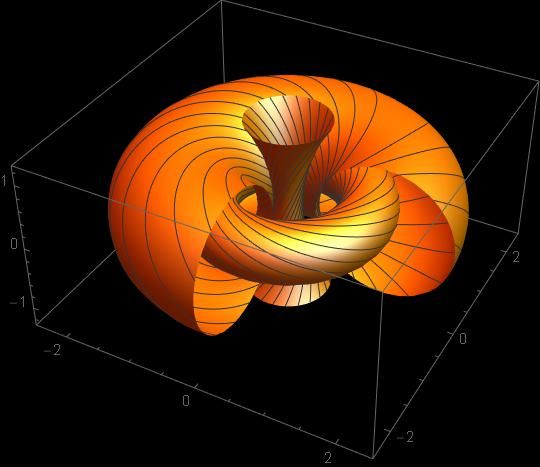
Widoczne są linie parametru psi. Teraz trzeba zaprzęgnąć wyobraźnię. Ta pionowa trąbka, to kawałek OGROMNEGO torusa. Zamyka się gdzieś poza obrębem układu słonecznego :)
Kąt psi okaże się ważny - "kwantowa faza". Ale o tym w kolejnej notce.
W międzyczasie w moich notkach była nierównomierność. Pracowałem nad poprawianiem błędów w mojej pracy o algebrach Clifforda (gdzie też pojawia się coś w rodzaju kwantowej fazy). Wczoraj ukończyłem to poprawianie i dziś już jest dostępna nowa wersja:
https://arxiv.org/abs/2103.09767
P.A. Ale się rąbnąłem! Po komentarzu Tichego narysowałem całą trąbke. I okazało się, że mieści się w zakresie (-5,5) , podczas gdy obrazek trzech torusów był w (-2.5,2.5):
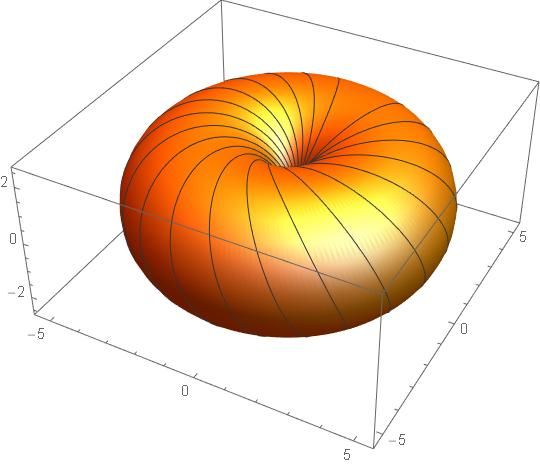
A tu dodałem linie parametru theta:
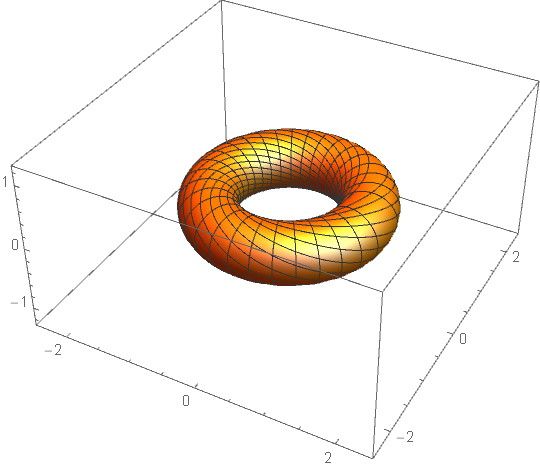
Naukowiec, zainteresowany obrzeżami nauki.
Katalog SEO Katalog Stron
map counter
Życie jest religią.
Nasze życiowe doświadczenia odzwierciedlają nasze oddziaływania z Bogiem.
Ludzie śpiący są ludźmi małej wiary gdy idzie o ich oddziaływania ze wszystkim co stworzone.
Niektórzy ludzie sądzą, że świat istnieje dla nich, po to, by go pokonać, zignorować lub zgasić.
Dla tych ludzi świat zgaśnie.
Staną się dokładnie tym co dali życiu.
Staną się jedynie snem w "przeszłości".
Ci co baczą uważnie na obiektywną rzeczywistość wokół siebie, staną się rzeczywistością "Przyszłości"
Lista wszystkich wpisów
Nowości od blogera
Inne tematy w dziale Technologie

