Półgrupy operatorów i mistyka

Przeglądając sieć trafiamy na matematyczne wyjaśnienie zjawiska epidemii:

„Ilu z nas trzeba zaszczepić, aby uniknąć epidemii? Matematyka masowych szczepień.”
….
Załóżmy, dla uproszczenia, że każdy chory, zanim nie wydobrzeje (albo umrze, bo i tak się może zdarzyć), zakaża średnio dwie zdrowe osoby. Liczba zakażonych podwaja się w każdym kroku - z dwóch chorych robi się czterech, z czterech - ośmiu itd. - i rośnie lawinowo. Matematycy mówią, że rośnie w sposób wykładniczy, bo tym wzrostem rządzi funkcja wykładnicza - w tym wypadku 2 do potęgi n, gdzie n jest liczbą osób zakażonych i rozsiewających zarazki.
….
Zaś z witryny eSzkola.pl dowiadujemy się, że
….
Funkcja eksponencjalna

Szczególnym przypadkiem funkcji wykładniczej jest tak zwana funkcja eksponencjalna (inne nazwy to eksponent lub eksponenta), w której parametrem a jest liczba Eulera, f(x) = e ^{x} . Równoznacznym oznaczeniem jest \exp(x).

Wykres funkcji e^x widoczny jest poniżej.

Funkcja eksponencjalna

Dziedziną funkcji eksponent jest zbiór liczb rzeczywistych, zbiorem wartości zbiór liczb rzeczywistych dodatnich.

Nie posiada ona miejsc zerowych.

Podobnie jak wszystkie funkcje wykładnicze postaci y=a^x przechodzi przez punkt (0,1), z kolei w jedynce przyjmuje wartość e, stąd do wykresu funkcji należy także punkt (1,e).

….

Licealista, który dowiedział się już co to jest pochodna, dowiedział się też przypuszczalnie, że funkcja eksponencjalna ma tę osobliwą własność, iż jest równa swojej pochodnej: czym większa jej wartość, tym szybciej rośnie: (exp(x))' = exp(x). Tajemnicza to funkcja, nadająca się do zakorkowania w butelce i wrzuceniu do morza.

Gdy rozpoczynałem moje studia doktoranckie jako fizyk teoretyk, mogłem wybrać materiał, którego chciałem się nauczyć. Mogłem wybrać potem egzaminatora i zdać z wyuczonego materiału egzamin. Jednym z pierwszych tematów do nauki jaki wybrałem była „analiza funkcjonalna”. Bardzo mi się ten dział matematyki podobał i wydawało mi się, że jego znajomość jest niezbędna gdy chce się opanować ze zrozumieniem rachunki wykonywane w zastosowaniach mechaniki kwantowej i kwantowej teorii pola. Analiza funkcjonalna to głównie przestrzenie Hilberta ( i ogólniejsze od nich przestrzenie Banacha), oraz teoria operatorów liniowych ( i algebr tych operatorów) w tych przestrzeniach. Jednym z pierwszych podręczników które zacząłem wtedy studiować była monografia Einar Hille, Ralph Phillips, „Functional Analysis and Semi-Groups”.

Urzekły mnie wtedy twierdzenia o tym jak to zamiana mnożenia na dodawania prowadzi do funkcji eksponencjalnej – i to dla operatorów, a nie tylko dla zwykłych liczb! Dla dopełnienia mojej nauki zaliczyłem wtedy także wykład z analizy harmonicznej a egazamin, jak pamiętam, zdałem z niezłym wynikiem u profesora Andrzeja Hulanickiego (który potem był jednym z recenzentów mojej rozprawy doktorskiej).

Andrzej Hulanicki was one of the most distinguished Polish mathematicians of the second half of XX century.

Taki to ze mnie był „fizyk”! I taki to jest do dziś. Forsuję mój światopogląd i zacieram różnicę pomiędzy matematyką a fizyką. Prawda, moim zdaniem, tkwi w matematyce, w jej twierdzeniach i w dowodach. No i w naszej intuicji bez której nie byłoby ani matematyki, ani twierdzeń, ani ich dowodów.

Oto odpowiedni fragmenty z monografii Hille i Phillipsa:

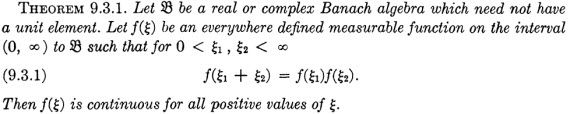
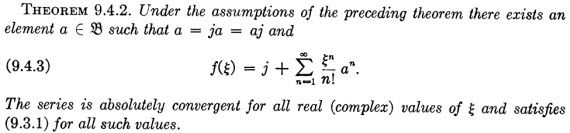
Wracam teraz do mojej zamiany mnożenia na dodawanie i przechodzę do dowodu Lematu 3 z Algebry Bourbakiego, Chapter 9 – o czym już pisałem w notce „Bourbaki a kryptografia”:

Lemat 3. Jeśli F i G są dwiema formami biliniowymi VxV → K, wtedy

(3) λ_F λ_G = λ_G λ_F = λ_F+G.

Dla każdej formy biliniowej F odwzorowanie λ_F jest wzajemnie jednoznacznym odwzorowaniem przestrzeni liniowej T(V) na siebie.

Wprowadzone w poprzednich notkach operatory zamieniają mnożenie w sparametryzowanej formami biliniowymi rodzinie operatorów λ_F na dodawanie ich parametrów. I chciałoby się pokazać, tzn. udowodnić matematycznie, że mamy tu do czynienia z funkcją eksponencjalną jak w przytoczonym powyżej twierdzeniu z monografii Hille i Phillipsa. Tyle, że ja chcę to zrobić uogólniając kontekst: miast przestrzeni liniowych nad ciałem liczb rzeczywistych czy zespolonych, jak w podręczniku, chcę to zrobić dla przestrzeni liniowej nad dowolnym, także skończonym, polem liczb..... Ot, takie mam widzimisię, tak oto chcę „sforsować mój światopogląd”.

Najpierw wszak dowód Lematu 3, idąc śladami Nicolasa Bourbakiego

W Algebrze Bourbakiego dowód Lematu 3 ma sześć linijek wygląda tak:

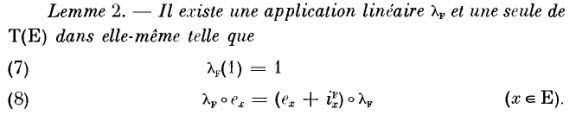
Właściwie nie ma po co bym ten dowód powtarzał. Te sześć linijek dowodu u Bourbakiego wystarczy. A jeśli ktoś będzie miał jakieś pytania – chętnie odpowiem. By jednak upodobnić naszą sytuację do tej u Hille i Phillipsa, zauważny, że dla F = 0 (co odpowiada ξ = 0 u Hille-Phillipsa) mamy λ_F = I – odwzorowanie identycznościowe. Wynika to z definicji λF = we wzorach (7), (8). Wiemy z Lematu 2, że mające te własności λ_F = jest jedyne. Zaś dla F=0 mamy i_x^F=0 (bowiem F → i_x^F) jst liniowe, stąd λ_F = I spełnia wlaśność (9). Własność (8) jest oczywista. W formułach u Hille-Phillipsa kładziemy więc j = I i mamy piękną funkcję eksponencjalną. Tyle, że w formule (9.4.3) nie wolno nam dzielić przez n!, bowiem dla ciał o charakterystyce skończonej n! może być zerem!

Nie można więc tego problemu rozwiązać bez forsowania jakiegoś nie całkiem zwykłego światopoglądu (jak na przykład, że matematyka potrzebna do opisu naszej niematerialnej rzeczywistości może wymagać liczb pierwszych i pól skończonych). Moi znajomi z Kasjopei stwierdzili bowiem kiedyś w rozmowie ze mną, że to właśnie wśród liczb pierwszych obracają się mistycy

Patrz witryna Matthew R. Watkinsa „Secrets of Creation”, a tam http://empslocal.ex.ac.uk/people/staff/mrwatkin/isoc/cassaeopians.htm

Inną motywacją do zajęcia się serio polami skończonymi mogą być mistyczne publikacje Matti Pittkanena, np. „Prime numbers in pregeometry” . Patrz także:

CATEGORY: The Nature of Time Essay Contest (2008)
TOPIC: About the Nature of Time by Matti Juhani Pitkänen