Bourbaki a kryptografia

Przyszła dziś wreszcie kolej na zapowiadaną przeze mnie kandydatkę na funkcję eksponencjalną „ e do X” - w polach skończonych. Trochę to się wiąże z kryptografią. W Wikipedii na przykład, pod hasłem „logarytm dyskretny” z łatwością znajdziemy, że „Trudność znalezienia logarytmu dyskretnego jest podstawą istnienia wielu algorytmów kryptograficznych, takich jak ElGamal i protokół Diffiego-Hellmana czy kryptografia oparta na krzywych eliptycznych. ” Rzecz w tym, że podnoszenie do potęgi w ciałach o charakterystyce skończonej jest „rzeczą łatwą”, jednak ze względu na branie operacji „modulo” wyniki tego podnoszenia zachowują się, jak na naszą ludzką inteligencję, chaotycznie, stąd branie funkcji odwrotnej, logarytmu, jest „obliczeniowo trudne”. Tak trudne, że dla dostatecznie dużych wykładników bez klucza praktycznie niemożliwe. Stąd zastosowania w kryptografii. Moja kandydatka na funkcję eksponencjalną, która się dziś pojawi, to co prawda problem innego rodzaju, jednak trudności w jej zdefiniowaniu są podobnej natury – zachowanie się potęg w ciałach skończonych powoduje to, że jak dotąd nikt skutecznie tej funkcji nie zdefiniował. To co poniżej jest moją przymiarką i to w bardzo szczególnym przypadku. Być może kryptografowie z NSA mój problem już dawno zresztą rozwiązali? Cytuję z monografii (str 62):

„Of course, one never knows what cryptanalytic breakthroughs have been made by the scientists at the National Security Agency, since virtually all of their research is classiﬁed. The NSA is reputed to be the world’s largest single employer of Ph.D.s in mathematics.”

Oczywiście nikt nie ma najmniejszego pojęcia o tym jakich to kryptoanalitycznych przełomów dokonali naukowcy z amerykańskiej Narodowej Agencji Bezpieczeństwa. NSA znana jest z tego, że zatrudnia największą na świecie liczbę matematyków z doktoratami.

Notka niniejsza jest kontynuacją serii trzech poprzednich notek:

1) Ślizgawka w charakterystyce dwa

2) Mateusz, Pani i Pies odkrywają anty-różniczkowania

3) Matematyka w krainie elfów

Nie będę wracał do ich treści, będę zakładał, że jest znana i rozumiana. W notce „Mateusz, Pani i Pies odkrywają anty-różniczkowania” wprowadziliśmy, dla każdego f z V* anty-różniczkowanie i_f algebry tensorowej T=T(V).

Dziś wprowadzimy najpierw wariację na ten temat. Przypuśćmy, że F:V x V → K jest formą biliniową na V. To znaczy, że odwzorowanie (x.y) → F(x,y) jest liniowe zarówno w x jak i w y.
Powiedzmy, że mamy formę biliniową F i że mamy wektor x należący do V. Wtedy możemy zdefiniować formę liniową f_x,F: V → K zdefiniowaną jako

f_x,F(y) = F(x,y)

Możemy wtedy wziąć anty-różniczkowanie i_fx,F względem tej formy, gdzie powinniśmy użyć podwójnego obniżenia wskaźnika, co jest niewygodne. Dlatego (za Bourbakim) wprowadzamy oznaczeni i_x^F dla oznaczenia tego anty-różniczkownia. Z definicji anty-różniczkowań i_f wynikają własności definiujące ixf

i_x^F (1) = 0
i_x^F (y⊗v) = F(x,y)v – y⊗ i_x^F(v)
(patrz formuła (M) w notce „Mateusz, Pani i Pies odkrywają anty-różniczkowania”)
Dodatkowo odwzorowania x,F → i_x^F są liniowe w x i w F, zaś i_x^F i i_x'^F' ze sobą antykomutują.

I teraz pojawia się na scenie mój kandydat na funkcję eksponenencjalną: operator λ_F. Przytaczam dwa lematy z Bourbakiego. Ich dowody podam w następnej notce. Najpierw w języku rosyjskim książki Бурбаки Н. Алгебра. Модули, кольца, формы

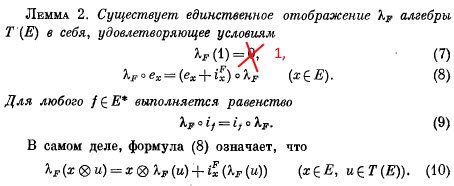
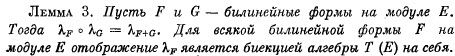
Uwaga: Dzięki zwróceniu mojej uwagi w komentarzu przez Bjaba poprawiłem błąd w formule (7) wydania rosyjskiego.

A gdy ktoś nie zna rosyjskiego, w języku francuskim (N. Bourbaki, Algebre, Chapitre 9, Springer 1981):

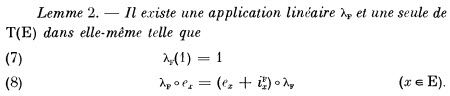
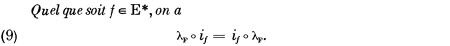
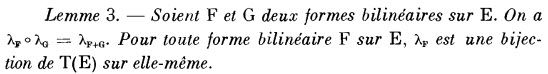
I wreszcie w tłumaczeniu na polski:

Lemat 2. Niech F: VxV → K będzie formą biliniową na przestrzeni liniowej V nad ciałem K. Istnieje wtedy jedno i tylko jedno odwzorowanie liniowe λ_F algebry tensorowej T(V) w siebie λ_F: T(V) --> T(V) takie, że

(1) λ_F(1) = 1
(2) λ_F e_x =(e_x+i_xF)λ_F, x należy do V

Lemat 3. Jeśli F i G są dwiema formami biliniowymi VxV → K, wtedy

(3) λ_F λ_G = λ_G λ_F= λ_F+G.

Dla każdej formy biliniowej F odwzorowanie lambda F jest wzajemnie jednoznacznym odwzorowaniem przestrzeni liniowej T(V) na siebie.

Własności (1) oraz (3) charakteryzują funkcję eksponencjalną gdy pracujemy z liczbami rzeczywistymi (patrz własność 5 w artykule w Wikipedii „Characterizations of the exponential function” ).

To zdanie powyżej było w wersji oryginalnej tej notki. Powinno być natomiast: Własność (3) jest najważniejszą własnością charakteryzującą funkcję eksponencjalną. Patrz własność 5 w artykule w Wikipedii „Characterizations of the exponential function”

Tutaj jednak zamiast liczb rzeczywistych mamy dowolne ciało Wikipedia się tak ogólnego przypadku nie ima. Trzeba więc kombinować samemu. Jednak najpierw, w następnej notce, zobaczymy jak się dowodzi tych dwóch lematów dla dowolnego ciała K. To czy ciało K jest skończone czy nie, to jaka jest jego charakterystyka – nie ma, jak zobaczymy, w tym dowodzie znaczenia.