Mateusz, Pani i Pies odkrywają anty-różniczkowania

Wszelki rozwój odbywa się poprzez ścieranie się przeciwieństw. Teza-antyteza-synteza.  Dialektyka. Cytując z Encyklopedii PWN:

„W filozofii nowożytnej dialektykę jako teorię rozwoju rzeczywistości przez przeciwieństwa odnowiła renesansowa filozofia przyrody (G. Bruno, Mikołaj z Kuzy); pojęcie dialektyki występowało w klasycznej filozofii niemieckiej: u I. Kanta (antynomie), J.G. Fichtego, F.W. Schellinga, zwłaszcza u G.W.F. Hegla — jako teoria rzeczywistości stanowiącej proces rozwoju ducha przez powstawanie i znoszenie przeciwieństw oraz metoda rozumowania polegająca na przechodzeniu od danego pojęcia (teza) do jego przeciwieństwa (antyteza) i łączeniu ich w wyższą jakość (synteza).

I tak jest u nas  Mamy przestrzeń liniową V – jej elementami są „wektory” (tezy). Mamy przestrzeń liniową V* - przestrzeń dualną, przestrzeń liniowych funkcjonałów na V o wartościach w ciele K. Elementami przestrzeni V* są „formy” (antytezy). Działając formą f ∊ V* na wektor x ∊ V otrzymujemy element ciała K (syntezę) f(x) ∊  K. Forma wchłania wektor i z tego związku rodzi się ciało. Puszczając wodze fantazji fizyka – jeśli elementy przestrzeni V interpretować jako stany „cząstek”, to elementy przestrzeni V* interpretować możemy jako stany anty-cząstek. Antycząstka anihiluje cząstkę, z wektora x i ko-wektora f tworzy się liczba f(x).  Tyle słowami, tyle powie poeta. Jednak:

W klasie jest zawsze więcej kandydatów na kiepskich poetów niż na wybitnych matematyków, co wzmaga niecierpliwość u mistrzów tej nauki. Znakomity matematyk nie może tego pojąć, że inni nie mogą pojąć wspaniałych zawiłości, dlatego tak patrzy na ludzi jak na nieznośne błędy w mądrym rachunku.

To cytat z powieści Kornela Makuszyńskiego „Szatan z siódmej klasy”. Mateusz z 2c jest kandydatem na wybitnego matematyka i choć nie stroni od poezji, chce być kimś więcej niż tylko poetą. Chce być wybitnym matematykiem, przede wszystkim wybitnym fizykiem (teoretykiem oczywiście). Chce rozumieć. A rozumieć się nie da bez algebry. Wejdźmy więc w tę algebrę. Przy tym algebra jest rodzaju żeńskiego, zatem współżycie z nią nie jest rzeczą łatwą. Inny cytat z „Szatana z siódmej klasy”:

Czemu ta dziewczyna ciągle płacze? - pomyślał profesor. - Dziwnym stworzeniem jest kobieta! Smutno jej było - płakała, teraz znowu płacze, bo jej wesoło. Jest to ponad rozumne pojęcie, że dwa odmienne uczucia kobieta umie tym samym wyrażać sposobem..."

I dziwnym tworem jest algebra. Wydaje się być ponad rozumem, ale warto w jej zrozumienie, choć częściowe, włożyć nieco (a nawet więcej niż nieco) trudu.

W poprzedniej notce wprowadziliśmy matematyczne operatory anihilacji. Przypomnijmy je i pobawmy się nimi. Pośledźmy je, dowiedzmy się po cichu o nich – jak na detektywów przystało.
Przypomnijmy z poprzedniej notki:

Niech f będzie elementem przestrzeni dualnej V*. Wtedy operator anihilacji i_f definiujemy tak jak to jest u Bourbakiego. Oto odpowiedni fragment z  rosyjskiego wydania jednego z tomów algebry Bourbakiego (Бурбаки Н. Алгебра. Модули, кольца, формы, str. 475):

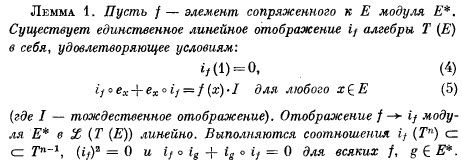
Po polsku będzie to tak: Istnieje jedyny liniowy operator i_f w T spełniający następujące warunki:

i_f 1 = 0,            (*)
i_f e_x + e_x i_f = f(x) I dla każdego x z V.    (**)
Przyglądając się tym formułom powyżej zauważamy, że mamy tam dwa podobne symbole 1 i I. Symbol I to operator tożsamościowy działający na elementy algebry tensorowej T. Zaś 1 to jedynka w ciele K, liczba 1, element algebry tensorowej T, ściślej, element  z T⁰, interpretowany jako stan z zerową ilością cząstek. Zatem, wnioskujemy, dla x,y,u,v ∊ V:

I1 = 1, Ix = x, I x⊗ y = x⊗y

Zaś 1+x to superpozycja stanu próżni i stanu jednocząstkowego, 1+x⊗y+u⊗v to superpozycja stanu próżni i stanu dwucząstkowego (niejednorodnego).

W formule (**) mamy równość dwóch operatorów. Możemy zatem lewą i prawą stroną formuły podziałać na jakiś wektor z T (bo T to także przestrzeń liniowa) , powiedzmy na wektor 1.

(i_f e_x +e_x i_f)1 = f(x)I1

po prawej mamy I1=1, oraz f(x)1=f(x), bo f(x) i 1 są elementami ciała K. Po lewej korzystamy ze wzoru z poprzedniej notki definiującego operatory kreacji e_x. Operator e_x to operator mnożenia (tensorowego z lewej) przez x. Zatem i_fe_x1=i_f x. Z drugiej strony z (*) mamy, że i_f1=0. Zatem nasza formuła daje

i_f x = f(x)

Mamy już więc: i_f 1 = 0, i_f x = f(x). Podziałajmy teraz obiema stronami  równości (**) na dowolny wektor v z T. Mamy

i_f e_x v + e_x i_f v= f(x)v

Co możemy zapisać w postaci

i_f (x⊗v) = i_f(x) v – x⊗i_f(v)                                        (M)

Tu Mateusz przypomniał sobie definicję operatora różniczkowania z notki o polach wektorowych i go olśniło: pochodna iloczynu to pochodna pierwszego razy drugi plus pierwszy razy pochodna drugiego. Eureka! Operator i_f działa jak operator różniczkowania, tyle, że z minusem a nie z plusem. „Wymyśliłem operator anty-różniczkowania”, oznajmił Mateusz swym kolegom z agencji detektywistycznej. Wygrałem 50 zł.

Ale tak dobrze nie jest, pokazał bowiem Mateusz swój operator anty-rózniczkowania Pani, a Pani się tylko uśmiechnęła i dała Mateuszowi kolejne zadanie: A co jeśli zamiast x będzie w formule (M) dowolne jednorodne u z T^k?

No i masz ci los! Szóstka już była w kieszeni, a tu okazuje się, że dalej trzeba się napracować i w dodatku nie bardzo wiadomo jak to zadanie zrobić? Od czego zacząć? I tak głowiąc się wyszedł Mateusz z psem na spacer. Pies szczeknął „Hau!”. No właśnie, „How?”. I tu przyszła Muza i podpowiedziała: zastąp dowolne v przez y⊗v! Wrócił Mateusz do domu i zaczął zastępować. Skoro (M) zachodzi dla dowolnego v z T, to zachodzi też dla y⊗v, gdzie y jest dowolne z V, zaś v jest dowolne z T:

i_f (x⊗y⊗v) = i_f(x) y⊗v – x⊗i_f(y⊗v)

W członie x⊗i_f(y⊗v) możemy skorzystać z (M)

i_f(y⊗v) = i_f(y)⊗v – y⊗i_f(v)
Zatem

x⊗i_f(y⊗v) =x⊗i_f(y)⊗v – x⊗y⊗i_f(v)

Czyli

i_f (x⊗y⊗v) = i_f(x) y⊗v –x⊗i_f(y)⊗v + x⊗y⊗i_f(v)

Jednak z (M) pierwsze dwa człony to i_f(x⊗y), więc

i_f (x⊗y⊗v) = i_f(x⊗y)v +x⊗y⊗i_f(v)

I znów mamy regułę różniczkowania iloczynu, jednak tym razem z plusem. I trzeba drugi raz wychodzić z psem na spacer..... No tak, ale teraz znów możemy zastąpić v przez z⊗v. Reguły są proste, jak w grze w szachy!

Szybki rachunek daje:

i_f (x⊗y⊗z⊗v) = i_f(x⊗y⊗z)⊗v -x⊗y⊗z⊗i_f(v)

I teraz wszystko staje się jasne! Dla u z T^k mamy

i_f(u⊗v)=i_f(u)⊗v+(-1)^k u⊗i_f(v)  (MM)

I to jest prawdziwe ogólne anty-różniczkowanie! (Patrz  tutaj). I upragniona szóstka. No, prawie. Bowiem by dostać szóstkę trzeba stąd wykazać, że dla dowolnych x₁,...,x_k z V mamy

i_f(x₁⊗...⊗x_k) = ∑ _i=1 ^k (-1)ⁱ⁺¹ f(x_i)x₁⊗...⊗[x_i]⊗...⊗x_k

gdzie x_i w nawiasie kwadratowym, [x_i], oznacza, że ten człon w iloczynie opuszczamy.

Teraz już znamy działanie i_f na wszystkich elementach jednorodnych, zatem i, przez liniowość, na całym T. Szóstka!

Nie tylko patrzył bystrze, lecz i widział bystrze. Ze spokojną, cierpliwą namiętnością obserwował wszystko i wszystkich. Sklejał z przedziwną zręcznością niedopowiedziane słowo, ułamki zdarzeń, okruchy i szczątki i umiał skleić z tego znikomego materiału prawdopodobną całość.

Kornel Makuszyński, Szatan z siódmej klasy