Ślizgawka w charakterystyce dwa

Obiecałem, zainspirowany przez dyskusję pod poprzednią notką, że przedstawię, maksymalnie prosto problem z pogranicza algebry i teorii liczb, który od miesięcy nie daje mi spać. I że przedstawię ten mój problem w możliwie prosty sposób, tak by nawet nieleniący się licealista (choć dziś trudno takiego znaleźć), jak i jego Pani profesor,  mogli mój problem zrozumieć. I tak też zrobię.

…. Tak pisałem jeszcze 4-go grudnia. Potem, 5-go grudnia popadłem w czarną rozpacz. Doszedłem do wniosku, że się pośliznąłem.

Gdy upadnę niezgrabnie,
wtedy czuję dokładnie
jakie ostre są moje hokeje.

Po czym 6-go grudnia, po żmudnych rachunkach,  po dwóch nieprzespanych nocach, znów pojawiła się we mnie nadzieja i zmieniłem swój zamiar. Początek tekstu będzie jak go pisałem 4-go lecz bardzo szybko dam spokój z uproszczeniami „dla licealisty”. Będę musiał potraktować mój problem ogólniej niż zamierzałem, zatem i bardziej abstrakcyjnie.  Zatem bardziej dla choć trochę zaawansowanego w algebrze studenta aniżeli dla zajętego zbieraniem piątek i szóstek licealisty, czy zajętej uczeniem i wychowywaniem licealistów Pani profesor. Cóż – tak wypadło. Nie moja to wina.

Oto początek z 4-go grudnia:

Polem bitwy jest algebra tensorowa T=T(V) nad przestrzenią liniowa V. Przestrzeń liniowa V jest nad ciałem K. To ciało K, w fizyce zarówno klasycznej jak i kwantowej, to zwykle ciało liczb rzeczywistych lub zespolonych. Jednak mój problem do rozwiązania zaczyna się tam gdy ciało K jest ciałem o skończonej charakterystyce p. Na przykład liczby całkowite modulo p, gdzie p jest liczbą pierwszą są takim ciałem. A u nas, by rzecz możliwie uprościć, wybierzemy ciało liczb całkowitych modulo 2. Ciało nasze będzie miało więc dwa elementy, 0 i 1, K= Z2 ={0,1}, przy tym dodawanie jest modulo 2, czyli umawiamy się, że 1+1=0.

Algebra tensorowa, w ogólnym przypadku, jest lekko trudna ( można zajrzeć do angielskiej Wikipedii tutaj ). Jednak znacznie się upraszcza gdy przestrzeń V jest jednowymiarowa. Gdy V jest jednowymiarowa, można V utożsamić z ciałem K, zatem bierzemy V=K. Wtedy  K⊗K = K i algebrę tensorową możemy utożsamić z sumą prostą

T=T(V) = K ⊕ K ⊕  K ⊕  ….

Elementami T są wtedy ciągi (a0,a1,a2, …) elementów z K, przy tym interesują nas ciągi które od pewnego miejsca mają same zera (tak wynika z definicji algebry tensorowej). W przypadku gdy  K=Z2, będą to ciągi zero-jedynkowe, na przykład (1,0,0,1,1,0,0,0,....) . I to będzie nasza T. Możemy przy tym utożsamić naszą T z algebrą wielomianów o współczynnikach z ciała K (tak wynika z definicji algebry tensorowej, w którą to definicję nie mamy potrzeby się wgłębiać) w jednej zmiennej nieokreślonej x. Tak więc ciąg  (a0,a1,a2, …) utożsamiamy z wielomianem

a(x) = a0+a1 x+a2 x^2+....

Bardzo proste, prawda? Wielomian to każdy licealista zna, potrafi wielomiany dodawać i nawet mnożyć.

Koniec początku z 4-go grudnia.

Nie chcę zbyt wcześnie zejść do Z2. I nie chcę zejść do szczególnego przypadku gdy V jest jednowymiarowe. To znaczy chciałbym, ale raczej nie mogę. Wydaje mi się, by zademonstrować o co mi idzie, że V musi być co najmniej 4-wymiarowe. W dalszym ciągu wytłumaczę dlaczego (choć sam nie całkiem to rozumiem). Zatem najpierw przedstawię przypadek ogólny, a do szczególnego przejdę na końcu.

Zatem mamy algebrę tensorową T(V), gdzie V przestrzeń liniowa nad dowolnym ciałem K. Tichy będzie wiedział o czym piszę. Bjab zapewne także. Lecz może nie tylko oni? Taką mam cichą nadzieję.

Uwaga: Algebry tensorowej uczyć się trzeba na chłodno. Wszelkie stany emocjonalne, zakochania itp. naukę algebry tensorowej kompletnie uniemożliwiają, nawet przy skądinąd dobrych chęciach.

Bierzemy więc ogólna algebrę tensorową

T = K ⊕ V ⊕ V⊗V ⊕ V ⊗V⊗V ⊕ …

T jest sumą prostą kolejnych potęg tensorowych przestrzeni V:

T = T⁰ ⊕ T¹ ⊕ T² ⊕ T³ ⊕ …

gdzie T0=K, T¹=V, T² =  V⊗V, T³ =  V ⊗V⊗V, itd.

Fizyk, który przeszedł przez kurs mechaniki kwantowej wielu ciał lub otarł się o „drugie kwantowanie”   powie: mamy przestrzeń Focka dla cząstek rozróżnialnych (choć prawdopodobnie na studiach od razu przechodzi się do cząstek nierozróżnialnych, bozonów lub fermionów). T^k to przestrzeń k-cząstkowa.

Mnożenie w algebrze T jest proste, np.:

(x⊗y)(z⊗u⊗v)=x⊗y⊗z⊗u⊗v

Algebra T ma zatem Z-gradację: T^k T^l ⊂  T^k+l. Jednak dla nas ważniejsza będzie Z2 gradacja. Będziemy inaczej traktować T^k z k parzystym (k=0,2,4,6,...) i z k nieparzystym (k=1,3,...). Czemu tak? Zobaczymy to za chwilę gdy zdefiniujemy operatory anihilacji przypominające swą konstrukcją operatory anihilacji dla fermionów. Najpierw jednak zdefiniujmy operatory kreacji.

W fizyce operatory kreacji i anihilacji oznacza się zwykle literami a* i a. My bawimy się abstrakcyjną matematyką, więc wezmę oznaczenia od Bourbakistów. Operator kreacji cząstki w stanie x oznaczę symbolem e_x. Niech x będzie wektorem w V, wtedy e_x zdefiniowane jest jako mnożenie tensorowe z lewej strony przez x. Dla dowolnego u z T definiujemy

e_x u = x⊗u

W szcególności

e_x1= x.

Tutaj 1 jest elementem z K=T⁰. Fizyk może powiedzieć, że jest to stan z zerową liczbą cząstek, czyli „stan próżni”.

Działając operatorem e_x na dowolny wektor z T^k otrzymujemy wektor z T^k+1 – zwiększamy liczbę cząstek o 1.

Wprowadzimy teraz opeartory anihilacji. W fizyce V jest przestrzenią Hilberta, zatem wyposażoną w iloczyn skalarny, który się potem przydaje do wyliczenia prawdopodobieństw. Operatory anihilacji są wtedy „sprzężone” do operatorów kreacji (względem tego iloczynu skalarnego). U nas iloczynu skalarnego w V póki co nie ma, zatem i operatory anihilacji zdefiniujemy chytrze,  „po matematycznemu”. Zauważmy najpierw, że z definicji iloczynu tensorowego każdy wektor z T^k jest kombinacją liniową (lub po prostu: sumą) wektorów jednorodnych, tzn. wektorów postaci x₁⊗...⊗x_k. Jeśli więc chcemy zdefiniować operator liniowy działający na wektory z T^k, wystarczy zdefiniować go na elementach jednorodnych, a dalej rozszerzyć przez liniowość.

Niech f będzie elementem przestrzeni dualnej V*. Wtedy operator anihilacji i_f definiujemy tak jak to jest u Bourbakiego. Oto odpowiedni fragment z  rosyjskiego wydania jednego z tomów algebry Bourbakiego (Бурбаки Н. Алгебра. Модули, кольца, формы, str. 475):

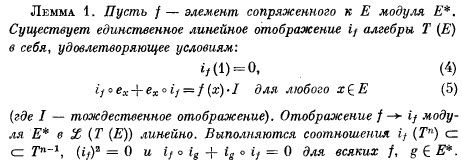
Po polsku będzie to tak:

Istnieje jedyny liniowy operator i_f w T spełniający następujące warunki:

i_f 1 = 0,
i_f e_x + e_x i_f = f(x) I dla każdego x z V.

Zauważmy, że w formule powyżej mamy antykomutator, więc jakby pachnie fermionami. Można teraz dowodzić tego twierdzenia, jak to jest u Bourbakiego. Lepiej jednak mi będzie podać jawną postać operatora i_f, którą nietrudno wyliczyć wiedząc, że takowy istnieje i jest jedyny. Wystarczy podać jak i_f działa na elementy jednorodne. Ale to już zrobimy w następnej notce. Podniosłem się z upadku i jadę dalej.