I tak przyszedł czas na algebrę, na wektory styczne, na rozmaitości i na różniczkowania. By to opanować trzeba wspiąć się na górę.
A czy na pewno trzeba? A trzeba. Bowiem nawet w Ewangelii wg św. Mateusza napisane jest „Nie zapala się też światła i nie stawia pod korcem , ale na świeczniku , aby świeciło wszystkim , którzy są w domu” . A algebra to światło, a światło świeci w ciemnościach. Więc wejdźmy po stopniach ku światłu, wbiegnijmy wręcz przeskakując po kilka stopni, stańmy na stopniu algebry, i stamtąd powoli schodźmy w dół, aż do sali gimnastycznej by różniczkując wrzucić wektory styczne do kosza rozmaitości.
Tylko co ten kot tu robi? Wołam na nią (bo to kotka a nie kot) „Pikabu the cat”. A ona do mnie mruczy „lambda F” wdrapuje się na biurko między mnie i monitor, i wywija bez przerwy ogonem krzywe algebraiczne.
No właśnie, bez algebry ani rusz i Mateusz o tym wie. Więc co to to jest ta algebra? Algebra to przede wszystkim przestrzeń liniowa – taka jak ta z tej poprzedniej notki. Jej elementy możemy mnożyć przez skalary i składać-dodawać do siebie. Jednak dochodzi też mnożenie elementów przez siebie. Jeśli A jest algebrą, jeśli skalarami są liczby rzeczywiste, to mamy określone działania
a + b oraz α a,
ale także ab
Przy tym obowiązuje zwykłe prawo rozdzielności względem dodawania – jak to wWikipedii każdy licealista z 2c może zobaczyć.
Mnożenie w algebrze na ogół nie musi być przemienne, zatem ab nie musi być równe ba. Nieprzemienna jest na przykład algebra kwaternionów. Nieprzemienne jest mnożenie macierzy. Inżynierowie na ogół o tym wiedzą. Licealiści? To nie jestem pewien. Zależy pewnie od szkoły. Jednak nam tutaj i teraz wystarczy algebra przemienna, algebra funkcji na rozmaitości.
Tylko co to ta rozmaitość? Rozmaitości straszą. U mnie w domu wczoraj obchodzono Halloween. Domownicy się poprzebierali. Tak to wyglądało
Rozmaitości mniej więcej są podobne, robią groźne miny. Jednak za groźnymi minami kryją się miłe i ciepłe głębie. Musimy zacząć od rozmaitości, nie ma rady. Przeskakujemy przez różniczkowania i nie pośliznąwszy się zatrzymujemy się na szczeblu Rozmaitości.
Od czego by tu zacząć? Nie ma rady, trzeba zacząć od R – liczb rzeczywistych. To najprostsza rozmaitość – jednowymiarowa. Dalej jest płaszczyzna, zwykle wyposażona we współrzędne kartezjańskie x, y – to rozmaitość dwuwymiarowa. To tak na zagrychę. Bowiem matematyk zaraz przyniesie globus i powie: sfera – to także rozmaitość dwuwymiarowa, tyle, że nie „płaska”. Jednak my sferami się nie będziemy na razie przejmować. Od razu przejdziemy do Rn – to najprostsza rozmaitość n-wymiarowa, gdzie n może być tu dowolne: 2,3,4,...,12, 137,...– byle skończone. Punkty tej n-wymiarowej rozmaitości opisywane są współrzędnymi: są to n-ki liczb rzeczywistych (x1,x2,...,xn).
Jednak gdyby tylko takie rozmaitości kotom i licealistom chodziły po głowie, nie byłoby to zbyt „rozmaite”. Są trzy ważne przyprawy do tego dania. Dwie z nich użyjemy, trzecią wzgardzimy – zepsułaby nam tylko nasz niewyrobiony jaszcze smak. Rozmaitość to zbiór punktów, które są opisywane współrzędnymi. Cała informacja o tych punktach to ich współrzędne. Rozmaitość jest n-wymiarowa gdy potrzeba nam n współrzędnych by wiernie te punkty opisać. Te współrzędne są z Rn, to n-ki liczb rzeczywistych. Taki układ współrzędnych na rozmaitości nazywamy „mapą”. Jednak nigdy nie będziemy się starać by mapa pokrywała całą rozmaitość. Wystarczy nam jeśli nasze n-ki współrzędnych opiszą tylko lokalne otoczenie interesującego nas punktu. Tak jak na tej mapie poniżej: tutaj aktualnie pływamy, objęcie współrzędnymi Antarktydy nas nie interesuje.
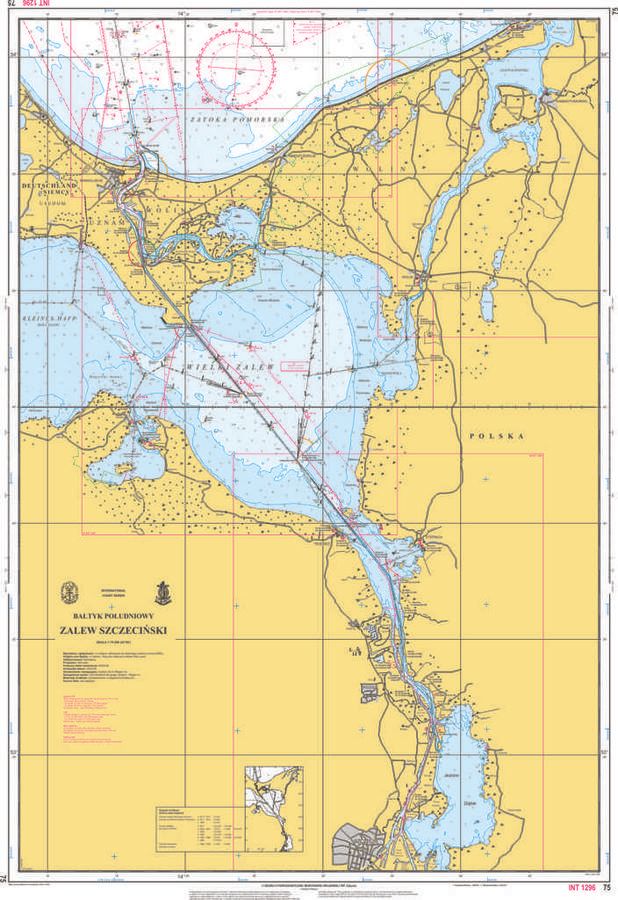
Po drugie, w sztuce pływania po rozmaitościach nie przywiązujemy się specjalnie do żadnej konkretnej siatki współrzędnych. Są różne siatki kartograficzne. Mają swoje zalety i wady. Żeglarz po rozmaitościach gdy trzeba użyje dowolnej siatki. Przy tym jedyne co jest ważne, to to, że jeśli (x1,x2,...,xn) jest dobrym układem współrzędnych, zaś (y1,....,yn) jest innym układem współrzędnych, byle współrzędne (y1,....,yn) były gładkimi (nieskończenie wiele razy różniczkowalnymi)i wzajemnie jednoznacznymi (lokalnymi) funkcjami współrzędnych (x1,x2,...,xn), i na odwrót, (x1, …, xn) są takimi funkcjami od (y1,...,yn), to nasz żeglarz nie będzie wybrzydzał. To znaczy musi być psychicznie przygotowany na niewybrzydzanie i być może musi przejść egzamin umienia posługiwania się każdą siatką. Gdy już jednak egzamin taki przejdzie, może posługiwać się tylko jedną. I my tak zrobimy.
A przy tym będziemy skromni i nie będziemy chcieli pokryć mapami całej planety naraz. Nasza planeta to Wszechświat, a co my tak naprawdę wiemy o tych częściach Wszechświata z których światło jeszcze nie zdążyło do nas dotrzeć?
Zatem skoncentrujmy się na jednej takiej mapie, której zasięg jest jakimś otwartym zbiorem U w Rn. Otwartym, to znaczy takim, że każdy punkt należy do niego wraz z pewnym swoim otoczeniem. Czy licealista wie co to jest zbiór otwarty? Czy wie co to jest otoczenie? Jeśli nawet nie wie, to kiedyś się dowie. Może nawet zajrzy do Wikipedii?
I teraz wchodzimy na stopień z algebrą. Interesować nas będą funkcje na rozmaitości, funkcje o wartościach rzeczywistych. Ponieważ rozmaitośc pokryliśmy siatką współrzędnych, nasze funkcje można uważać za funkcje f(x1,...,xn) od n zmiennych rzeczywistych. Krótko taką n-kę będę oznaczał literką x. Nasze funkcje można teraz dodawać do siebie
(f+g)(x)=f(x)+g(x)
Można mnożyc przez skalary (liczby)
(αf)(x) = α f(x)
ale także możemy mnożyć przez siebie
(fg)(x) = f(x)g(x).
A ponieważ mnożenie liczb rzeczywistych (a nawet i zespolonych) jest przemienne i łączne, to nasze funkcje tworzą algebrę przemienną (inaczej: abelową) i łączną.
I tą algebrą zajmiemy się w kolejnej notce, gdy wskoczymy na stopień różniczkowań w algebrze i dalej na stopień wektorów stycznych.
