Anna Komnena napisała w blogu Sówki55 i Myszulka takie oto słowa:
Święty Józef załamał ręce,
denerwują się w niebie święci,
teraz idą już nie Trzej Mędrcy,
lecz uczeni, doktorzy, docenci
Teraz wszystko całkiem inaczej,
to, co stare, odeszło, minęło,
zamiast złota niosą dolary,
zamiast kadzidła – komputer,
a zamiast mirry – video.
– Ach te czasy – myśli Pan Jezus –
nawet gwiazda trochę zwariowała
ale nic się już nie zawali,
bo wciąż Mamusia ta sama.
Ks. Jan Twardowski
Ciekwe są te spostrzeżenie księdza - poety.
U mnie Anna Komnena wpisała się łacińską sentencją autorstwa dwudziestoletniego Tychona Brahe: O crassa ingenia. O coeli spectratores.
Łaciny nieco łyknąłem kiedyś w V. chyba klasie zaledwie w zakresie podstaw ministrantury. Przetłumaczyć tego nie zdołam. Lecz niech żywi nie tracą nadziei! - miast tłumaczyć - wspomnę nieco późniejsze dokonania tegoż Tychona.
Należy On do grona trzech Mędrców: Tycho Brahe, Jan Kepler iIzaak Newton - którzy w tej kolejności, następny czerpiąc z dzieła poprzedniego, podczas siedemnastego wieku, jakby przypadkiem dokonali przełomu cywilizacyjnego w rozumach Ziemian.
Pierwszy z wyliczonych mędrców - spectrator - niejako przy okazji pracy jako astronom królewski na Zamku w Pradze, mierzył i notował skrupulatnie kąty pod jakimi w kolejne pogodne noce obserwował położenia planet na niebie.
Po co to robił? Po nic. Kto mu to czynić kazał? Nikt. Czy gdyby tego nie robił żyłoby mu się gorzej? Nie sądzę. Czy inni coś z tego wtedy mieli? Nic.
 Fot.1. Pomnik Tychona Brahe i Jana Keplera w Pradze
Fot.1. Pomnik Tychona Brahe i Jana Keplera w Pradze
Tychonowi asystował dwudziestoparoletni Jan Kepler. Zdolny był młody Jan wtedy na tyle, że staruszek Tycho (zmarł w okresie dokonywania tych obserwacji w wieku 54 lat) pomógł mu zostać w Pradze królewskim matematykiem.
Wspólny pomnik Brahego z Keplerem (fot.1) można obejrzeć pod hradczańskim zamkiem.
Po śmierci Tychona, przeświadczony że zbiór notatek Brahego ma nieznaną nikomu wtedy wielką wartość, zabrał się Jan Kepler do ich analizowania. Mądrze zauważył, że położenie Marsa w przestrzeni da się wyznaczyć z kątów widzenia Marsa z Ziemi zmierzonych w dwóch datach odległych od siebie dokładnie o marsjański rok. W tym czasie Ziemia, w czasie 11/6 roku przemieszcza się po swojej orbicie o 11/6 trajektorii obiegu Słońca. Powtarzając takie obliczenia dla Marsa będącego w różnych punktach nieba mógł Kepler geometrycznie wyznaczyć kolejne położenia Marsa w przestrzeni podczas jego obiegu wokół Słońca.
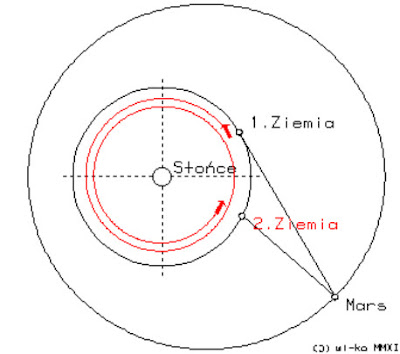
Fig.2 Wyznaczenie geometryczne położenia Marsa na jego wokółsłonecznej orbicie
Mając wiele pomiarów Brachego Kepler wyznaczył wiele punktów toru po którym Mars obiega Słońce.
Tu Kepler poza olśnieniem geometrycznym miał wiele szczęścia. Sprzyjało mu kilka faktów
- Ze względu na bliskość od Ziemi, łatwość obserwacji i względnie szybki ruch orbitalny zebrał Brahe na temat położeń Marsa dużo danych pomiarowych.
- Dobrą dokładność wyników obliczeń uzyskał Kepler dzięki temu, że orbita Ziemi jest niemal bliska okręgowi.
- Orbita Marsa jest silnie ekscentryczna i efekt jej eliptyczności dla fachowego matematyka Jakim był Jan Kepler łatwy był do odkrycia.
Ekscentryczność orbity Marsa była dla Keplera i ludzi jemu współczesnych wielkim zaskoczeniem. Po raz pierwszy od starożytności zauważono, że nie "doskonały" okrąg jest torem ciał niebieskich ale jakby "mniej doskonała" elipsa. Jako matematykowi nie było trudno mu zauważyć, że Słońce nie leży w środku tej elipsy ale w jej ognisku odległym od środka o parametr nazywany mimośrodem (ekscentrycznością).
Sformułował on to swoje odkrycie w formie Prawa Keplera (pierwszego) i uogólnił je dla wszystkich planet. Dziś wiemy że prawo to rządzi ruchem każdego poruszającego się orbitującego w Kosmosie ciała.
Patrząc na narysowane punkty wyznaczające tor Marsa wokół Słońca Kepler zauważył również, że planeta porusza się po orbicie tym szybciej im tor jej ruchu przebiega bliżej Słońca. Wnikliwe pomiary dały Keplerowi podstawy dla sformułowania jego Drugiego Prawa.
Oba te prawa brzmią (według Wikipedii) następująco.
I Prawo. Każda planeta Układu Słonecznego porusza się wokół Słońca po elipsie, w której w jednym z ognisk jest Słońce.
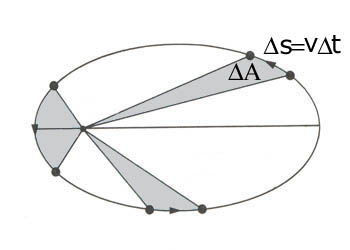
Rys.3. Ilustracja II.Prawa Keplera
II Prawo. W równych odstępach czasu, promień wodzący planety poprowadzony od Słońca zakreśla równe pola.
Pierwsze dwa prawa Kepler opublikował w 1609 roku. Przez dziesięć lat zmagał się on dalej ze zbiorami wyników pomiarów Tychona Brahe. Wreszcie przyszło kolejne olśnienie. Przysłużyła się temu modna wówczas numerologia. W różny sposób mnożąc, dzieląc i podnosząc do potęgi otrzymane z pomiarów liczby opisujące orbity planet Kepler zauważył, że:
Prawo III. Stosunek kwadratu okresu obiegu planety wokół Słońca do sześcianu wielkiej półosi jej orbity (czyli średniej odległości od Słońca) jest stały dla wszystkich planet w Układzie Słonecznym
Przez wiele lat te trzy prawa Keplera owiane były mgiełką tajemniczości.
Dopiero pół wieku później, również jakby przypadkiem, przebywający na wsi podczas panującej zarazy w Londynie dwudziestokilkuletni Izaak Newton, mając wiele wolnego czasu, zbudował matematyczny model prawa powszechnego ciążenia, z którego wprost można wyprowadzić wszystkie trzy prawa Keplera. Głównymi zasadami tych praw jest to, że każde dwie masy w przestrzeni, nawet gdy nie dotykają się do siebie, to przyciągają się nawzajem siłą proporcjonalną do iloczynu ich mas i odwrotnie proporcjonalną do kwadratu dzielącej je odległości oraz to, że siła działająca na ciało powoduje przyspieszenie jego ruchu proporcjonalne do iloczynu tej siły i masy ciała. Swoje rozważania na temat prawa powszechnego ciążenia opublikował Newton dwadzieścia lat później jako już zawodowy uczony uniwersytecki.
Warto wiedzieć, że nie fizyka ani matematyka dała Newtonowi prestiż wśrod współczesnych mu rządzących Anglią ludzi. Dzięki swoim badaniom w dziedzinie alchemii został on awansowany na urzędowe stanowisko szefa angielskiej mennicy. Wiele pracował nad przemianą metali w złoto potrzebne władcom Anglii. Chciał zapuścić się w Sudety w rejon Złotoryi, gdzie jak przypuszczał wytwarza się tajemnie złoto. Pracy nad alchemią złota do końca życia nie zdołał z sukcesem ukończyć.
 Fot.4. Dom rodzinny Izaaka Newtona.
Fot.4. Dom rodzinny Izaaka Newtona.
Jakież dzieła tych Mędrców są znamienne! Wiele się teraz mówi i pisze o nauce, o potrzebie zwiększenia jej finansowania, o grantach przydzielanych "uczonym" przez rządowych urzędników, marzy się jak by to było u nas dobrze gdyby dostawali oni jeszcze więcej pieniędzy. Czy napewno by to wynikom nauki pomogło?
Fotografie zaczerpnięte są z Wikipedii z wyjątkiem Fig.2. autorstwo mojego.

